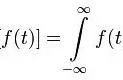如果你对信号处理感兴趣,说一天征服傅里叶有点夸张。当然,没有反覆实践和钻研数学, 您无法在一天里学会傅立叶变换的方方面面。无论如何, 这个在线课程将提供给您怎样进行傅立叶变换运算的基本知识。
能有效和能非常简单地领会的原因是我们使用了一种不太传统的逼近。重要的是你将学习傅立叶变换的要素而完全不用超过加法和乘法的数学计算! 我将设法在不超过以下六节里解释在对音像信号处理中傅立叶变换的实际应用。
步骤 1: 一些简单的前提
在下面,您需要理解以下四件最基本的事情: 加法,乘、除法。什么是正弦,余弦和正弦信号。明显地,我将跳第一二件事和将解释位最后一个。您大概还记得您在学校学过的“ 三角函数”[1] ,它神秘地用于 与角度一起从它们的内角计算它们的边长,反之亦然。我们这里不需要所有这些事,我们只需要知道二个 最重要的三角函数,"正弦" 和"余弦" 的外表特征。这相当简单: 他们看起来象是以峰顶和谷组成的从观察点向左右无限伸展的非常简单的波浪。

(附图一)
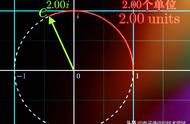
如同你所知道的,这两种波形是周期性的,这意味着在一定的时间、周期之后,它们看起来再次一样。 两种波形看起来也很象,但当正弦波在零点开始时余弦波开始出现在最大值。在实践中,我们如何判定我们在一个给定时间所观测到的波形是开始在它的最大值或在零? 问的好: 我们不能。实践上没有办法区分正弦波和余弦波,因此看起来象正弦或余弦波的我们统称为正弦波,在希腊语中译作"正弦类"。正弦波的一个重要性质是"频率"。它告诉我们在一个给定的时间内有多少个波峰和波谷。高频意味许多波峰和波谷, 低频率意味少量波峰和波谷:

(附图二)
步骤 2: 了解傅立叶定理
Jean-Baptiste Joseph Fourier 是孩子们中让父母感到骄傲和惭愧的的一个,因为他十四岁时就开始对他们说非常复杂的数学用语。他的一生中做了很多重要工作,但最重大的发现可能是解决了材料热传导问题。
他推导出了描述热在某一媒介中如何传导的公式,即用三角函数的无穷级数来解决这个问题(就是我们在上面讨论过的正弦、余弦函数)。主要和我们话题有关的是:傅里叶的发现总结成一般规律就是任意复杂的信号都能由一个个混合在一起的正弦函数的和来表示。
这是一个例子:

(附图三)
在这里你看到的是一个原始的信号,以及如何按某一确定的关系(“ 配方” )混合在一起的正弦函数混合物(我们称它们为分量)所逼近。我们将简略地谈论一下那份配方。如你所知,我们用的正弦函数愈多 其结果就愈精确地接近我们的原始信号波形。在“ 现实” 世界中,在信号连续的地方,即你能以无穷小的间 隔来测量它们,精度仅受你的测试设备限制,你需要无限多的正弦函数才能完美地建立任意一个给定的信 号。幸运地是,和数字信号处理者们一样,我们不是生活在那样的世界。相反,我们将处理仅以有限精度 每隔一定间隔被测量的现实世界的采样信号。因而,我们不需要无限多地正弦函数,我们只需要非常多。 稍后我们也将讨论这个“ 非常多” 是多少。目前重要的一点是你能够想象,任意一个在你计算机上的信号, 都能用简单正弦波按配方组成。
步骤 3: “ 非常多” 是多少
正如我们所知道的,复杂形状的波形能由混合在一起的正弦波所建立。我们也许要问需要多少正弦波来 构造任意一个在计算机上给定的信号。当然,倘若我们知道正在处理的信号是如何组成的,这可能至少是 一个单个正弦波。在许多情况下,我们处理的现实世界的信号可能有非常复杂的结构,以至于我们不能深 入知道实际上有多少“ 分量” 波存在。在这种情况下,即使我们无法知道原始的信号是由多少个正弦波来构 成的,肯定存在一个我们将需要多少正弦波的上限。尽管如此,这实际上没解决有多少的问题。让我们试 着来直观地逼近它: 假设一个信号我们有 1000 个样采,可能存在的最短周期正弦波(即多数波峰波谷在其 中)以交替的波峰波谷分布在每个采样内。因此,最高频率的正弦波将有 500 个波峰和 500 个波谷在我 们的 1000 个采样中,且每隔一个采样是波峰。下图中的黑点表示我们的采样,所以,最高频率的正弦波 以看起来象这样: