- 圆O上取一点A,过O作OA垂线,做OA中垂线交OA于B点
- 以O为圆心,OB为半径作圆,交OA垂线于C点。连接AC。
- 以C为圆心,OC为半径作圆交AC与D点。
- 以A为圆心,AD为半径作圆交AO与E点,交圆与F点。
E为OA黄金分割点,∠AOF=36°


最后连接AF,即为正10边形的边长。
结论:顶角为36°的等腰三角形ΔAOF为黄金三角形,即三条边的比例如下:

证明如下:
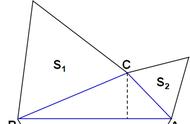
根据下图我们可以求出sin36°:

E为OA黄金分割点,∠AOF=36°


最后连接AF,即为正10边形的边长。
结论:顶角为36°的等腰三角形ΔAOF为黄金三角形,即三条边的比例如下:

证明如下:
根据下图我们可以求出sin36°:






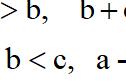







Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.