一、有切点、连半径、证垂直:
1、利用角度转换证垂直:
例题1、如图 AB是⊙O 的直径,点 C、D在⊙O上,∠A = 2 ∠BCD,点 E 在 AB 的延长线上,∠AED = ∠ABC 。
求证:DE 与 ⊙O相切。

图(1)
证明:

图(2)
2、利用勾股定理的逆定理证垂直:
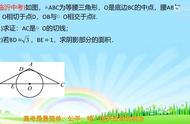
例题2、如图、在△ABC 中,以AB为直径的 ⊙O 交 AC于点 M ,弦 MN∥BC交AB于点E,
ME=1,AM=2,AE= √3。
求证: BC 是 ⊙O 的切线。

图(3)
证明:

一、有切点、连半径、证垂直:
1、利用角度转换证垂直:
例题1、如图 AB是⊙O 的直径,点 C、D在⊙O上,∠A = 2 ∠BCD,点 E 在 AB 的延长线上,∠AED = ∠ABC 。
求证:DE 与 ⊙O相切。

图(1)
证明:

图(2)
2、利用勾股定理的逆定理证垂直:
例题2、如图、在△ABC 中,以AB为直径的 ⊙O 交 AC于点 M ,弦 MN∥BC交AB于点E,
ME=1,AM=2,AE= √3。
求证: BC 是 ⊙O 的切线。

图(3)
证明:














Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.