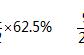平均数问题
专题解析:把几个不相等的数,在总数不变的条件下,通过一定的方式,使它们完全相等,求得的相等的数就是平均数。使它们完全相等这样的过程叫做平均。
可能有的同学疑惑了,老师你说的通过一定的方式,到底是什么方式呢?
我们说平均数问题是一个非常灵活性的问题,不管通过什么方式,只要满足两个条件:1、不改变总数。2、使大家相等就可以。
下面我们来看一下:
案例一:甲有14颗糖果,乙有8颗糖果,丙有8颗,丁有10颗糖果,我们可以通过什么方式使大家的糖果相等了?
回答1:将大家的糖果集中到一起重新分配,集中到一起共有14+8+8+10=40(颗),重新分配每个同学分到40÷4=10个。
回答2:将甲和乙的糖果集中到一起,重新分配,这样甲和乙都有11颗糖,再将丙和丁的糖果集中到一起,重新分配,这样丙和丁都各有9颗糖果。此时甲和乙再分别拿出1颗糖果给丙和丁,这样四个人的糖果数量也可以相等,即每个人10颗糖果。
同学们回答的都很好,第一个回答是我们常用的求解平均数的办法,即拿总数÷个数。
第二个回答实际上体现了移多补少的思想,先将甲、乙的糖果数量平均了一下,又将丙、丁的糖果数量平均了一下。发现甲、乙的糖果的平均数量高于四个人的糖果平均数量,当甲和乙拿出高出的部分平均分给丙和丁,丙和丁糖果的平均数量也将会变成
案例2:某次数学考试小明考了98分,小兰考了96分,小刚考了95分,小张考了80分,小红考了76分。这5位同学的平均分是多少了?
例1、合唱队里男同学的人数是女同学的一半,男同学的平均身高是154厘米,女同学的平均身高是160厘米,合唱队同学的平均身高是多少厘米?
思路分析:
方法一:可以先将男女同学的身高分别平均一下,则男同学的身高都相同,女同学的身高也相同了。由题意可知,女同学的人数是男同学人数的两倍,若我们将两个女生和一个男生组成一个小组,那么每组的情况都是一样的。每组当中平均每个人的身高是(160×2+154)÷3=158(厘米),因此合唱队同学的平均身高是158厘米。
方法二:符合题目要求的情况有很多种,可以是一个合唱队里男同学有1人,女同学2人,男同学的平均身高为154厘米,女同学的平均身高为160厘米。
亦可以合唱队里有2名男同学,4名女同学,男同学的平均身高为154厘米,女同学的平均身高为160厘米,等等。但是题目要求的是合唱队同学的平均身高,因此不管何种情况的结果都是一样的。
那我们设男同学有2人,女同学有4人,则合唱队同学的平均身高为(160×4+154×2)÷6=158(厘米)
题后反思:多思多练,很多题目我们可以从不同的角度去思考。
练习题
1、邮递员上山送信,上山时每小时行2千米,下山时每小时行3千米,他往返一趟的平均速度是每小时多少千米?
2、甲组数的个数是乙组数的2倍,甲组数的平均数是82,乙组数的平均数是76,甲、乙两组数的平均数是多少?
例2 、有甲、乙、丙、丁四个数,甲、乙、丙三个数的平均数是20,丁数比这四个数的平均数多12,求丁数。
思路分析:若丁数保留这四个数的平均数,将多出的12拿出来给其它3个数,其它3个数这时的平均数也会和自己一样,都达到了四个数的平均数。
解:20×3+12=72
72÷3=24……四个数的平均数
24+12=36……丁数
答:丁数的平均数为36
再尝试着用方程求解此题。
练习题
1、A、B、C、D、E、F 6个数,其中C、D、E、F这4个数分别为80、90、50、60,A和B的平均数比这6个数的平均数多10,问A和B的总和是多少?
2、小红与四名同学一起参加一次数学竞赛,那四名同学的成绩分别为78分、82分、91分、79分,小红的成绩比五人的平均成绩高6分,小红的成绩排在五人中的第几位?
3、若干个数的平均数是2013,增加一个数后,这些数的平均数仍是2013,则增加的这个数是多少?
4、文文在计算一列数的平均数时,错把117写成171,得到的结果为127,发现错误后重新计算得到正确结果是125.请问这列数共有多少个?
例3、博爱小学举行数学竞赛,把成绩排名次后,前5名平均分比前3名平均分少1分,前7名平均分比前5名平均分少2分,问第四、第五名得分之和比第六、第七名得分之和多几分?
思路分析:第四名和第五名得分之和=前五名的得分之和-前三名的得分总和,第六名和第七名得分之和=前七名得分之和-前五名得分之和。
根据题意,若我们将前3名的平均分设为a,则前5名的平均分就为a-1,前7名得平均分就为a-1-2=a-3。
第四和第五名得分之和=(a-1)×5-3a=2a-5
第六和第七名得分之和=(a-3)×7-(a-1)×5=2a-16
因此第四名和第五名得分之和比第六第七名得分之和多(2a-5)-(2a-16)=11(分)
答:第四、第五名得分之和比第六、第七名得分之和多11分。
练习题
1、育才小学某学期组织了六次数学测验,后四次的平均分比六次的平均分提高了3分,第一、第二和第六次的平均分比六次的平均分低了3.6分,那么前五次平均分比六次的平均分提高还是降低了多少分?
2、五(一)班数学考试平均成绩是91.5分,事后复查发现,计算成绩时将一位同学的98分误作89分计算了,经重新计算后,全班的平均成绩是91.7分,问五(1)班有多少名学生?
3、某班一次数学考试,所有成绩得优的同学的平均分数是95分,没有得优的同学的平均分数是80分,已知全班同学的平均成绩不少于90分,问得优的同学占全班同学的比例至少是多少?
4、有四个数,每次选取其中三个数算出他们的平均数再加上另外一个数,用这种方法计算了四次,分别得到以下四个数:86,92,100,106.那么,原来四个数的平均数是几?
5、体操比赛的裁判小组由若干人组成,每位裁判给选手的最高分不超过10分。第一名选手比赛后的得分情况是:全体裁判所给的平均分是9.64分;如果去掉一个最高分,其余裁判所给的平均分是9.60分;如果只去掉一个最低分,其余裁判所给的平均分是9.68分。那么,所有裁判所给的分数中最低分最少是多少分?这次比赛的裁判有多少名?
6、某次考试,林丽等7人的平均分是78分,其中得分最高的是97分,最低分是64分,林丽得了88分,余下的4人中3人得分相同;分数各不相同的5个人的平均分是80分,其中还有一个同学与别人的得分不同,他的得分是多少?
例4、某次数学竞赛原定一等奖10人,二等奖20人,现将一等奖中最后4人调整为二等奖,这样得二等奖的学生平均分提高了1分,得一等奖的学生的平均分提高了3分,那么原来一等奖平均分比二等奖的平均分多多少分?
思路分析:平均分的变化是由调整4人而引起的,所以要抓住这四个人进行分析。1、调整后一等奖的平均分提高了3分,说明原来求一等奖的平均分时,一等奖当中的前6人一共拿出3×6=18分给调整的这4人。
2、调整后二等奖的平均分提高了1分,说明在求新的二等奖平均分时,调整的这4个人一共拿出了20×1=20分,给原来的二等奖人员。
3、根据上述分析,若我们将原来一等奖的平均设为a,则调整的4个人脱离一等奖时,平均每个人变成了a-3×6÷4=a-4.5分。加入二等奖后调整的这4个人平均分变成了a-4.5-20÷4=a-9.5分,则原来二等奖的分数为a-9.5-1=a-10.5分。所以原来一等奖比二等奖多10.5分。
题后反思:调整这4个人,在一等奖的大家庭里平均每个人是a分,脱离一等奖变成了a-4.5分,加入二等奖后平均每人的分数变成了a-4.5-20÷4=a-9.5分。
练习题
1、乔治在某篮球赛最后一场比赛之前共获得88分,最后一场比赛他获得了23分,使得他本赛季的平均分为18.5分。本赛季乔治一共打了多少场比赛?
2、体操比赛有六位裁判评分,去掉最高分9.8分后,剩下五个分数的平均分就比原来的平均分少了0.05分,再去掉最低分9.42分后,剩下四个分数的平均分是多少?
3、今有若干个不同的正整数,它们的平均值是10,若去掉最大的一个,余下数的平均值为9。若去掉最小的一个,则余下的平均值为11。那么,这些数的个数至多是几个,这个最大的数可以是多少?
例5、老师在黑板上写了十三个自然数,让小明计算平均数(保留两位小数),小明计算出的答案是12.43,老师说最后一位数字错了,其它的数字都对,正确的答案是什么?
思路分析:因为最后一位数字错了,所以这十三个数正确的平均数最小是12.40,最大是12.49。若设这十三个数的和为a,那么12.40×13 ≤a ≤12.49×13,即161.2 ≤ a ≤162.37,又因为a是一个整数。所以a为162,正确的平均数为162÷13=12.46。
练习题
1、求17个自然数的平均数,使结果保留三位小数。小明算出的答案是9.415,这个结果最后一位数字不对,那么正确的答案应该是__________。
2、老师在黑板上写了18个自然数,让同学们求平均数,要求计算结果四舍五入保留两位小数。李静同学算得的答案是17.42,老师说最后一位数字错了,其它的数字都对。则正确答案是_____________。
同步练习
1、空间站上的5位宇航员轮流值班休息,值班岗位有2人。在60小时里,平均每位宇航员休息了_________时。
2、在99个连续的自然数中,最大的数是最小数的25.5倍,那么这个自然数的平均数是_________。
3、小马虎计算1~2006这2006个连续整数的平均数,在求这2006个,数的和时,他少算了其中的一个数,但他仍按2006个数计算平均数,结果求出的数比应求得的数小1.小马虎求和漏掉的数是_________。
4、五(1)班男生的平均身高是149厘米,女生的平均身高是144厘米,全班同学的平均身高是147厘米。则五(1)班的男生人数是女生人数的______倍。
5、跳水比赛中,有10位评委评分,规定:最后的分是去掉一个最高分和一个最低分后的平均数。10位评委给甲、乙两位选手打出的分数的平均数分别是9.75和9.76分,又知甲、乙两人最高分和最低分的平均数分别是9.83分和9.84分,那么最后得分________高。(填“甲”、“乙”或“一样”)
6、有四个数,任取其中三个数相加,得到四个不同的和,70,80,73,77.则这四个数分别为___________。
7、一次数学竞赛,满分是100分,某小组的8位同学得分都是整数,并且互不相同。已知这8位同学的平均分是90分,其中一位同学仅得62分,那么第五名至少得_________分。
8、某学生计算6个数的平均数,最后一步应该除以6,但是他将“÷”错写成“×”,于是得错误答案1800,那么正确答案是__________.
9、上午9:45,一辆公共汽车从始发站出发,半小时后,行驶总路程的6(
1
),公共汽车在这一段路程的平均速度是15千米/时,中午12:00,公共汽车到达终点站。则全程公共汽车行驶的平均速度是_________千米/时。
10、一辆汽车用全速行驶5分钟,又用半速行驶了6分钟,这11分钟的平均速度为800米/分。这辆汽车全速每分钟行驶_________米。
11、商店把10千克水果糖和若干千克奶糖混合在一起得到每千克12元的什锦糖。已知水果糖每千克10元,奶糖每千克16元,则这种什锦糖用了_________千克奶糖。
12、果品店将2千克酥糖,3千克水果糖,5千克奶糖混合成什锦糖。已知酥糖每千克4.40元,水果糖每千克4.20元,什锦糖每千克5.74元,那么奶糖每千克_________元。
13、通讯兵骑一辆摩托车行驶3000千米,除了车上的2只轮胎外还有一只备用胎,要使3个轮胎磨损程度相同,应有规律地把3只轮胎轮换使用,则到达终点时,每只轮胎行驶_________千米。
14、周某,小洋一家五人去登山,带了2个旅行包,5人轮流背,走了15千米,则平均每人背包走了_________千米。
15、在1~100这100个自然数中,所有是3的倍数的数的平均数是__________。
16、小华在计算出2003个数的平均数后,把所求得平均数也混在了原先的2003个数中,小华求得混在一起的平均数为2002,则原来的2003个数的平均数是_______。
17、有一列数,第一个数是105,第二个数是85,从第三个数开始,每个数都是它前面两个数的平均数,则第2007个数的整数部分_________。
18、某校有100个学生参加数学竞赛,平均得63分,其中男学生平均60分,女学生平均70分,男学生比女学生多______人。
19、在一次测验中,全班学生的平均分为72分,已知及格学生人数是不及格学生人数的4倍,及格学生的平均分是80分,不及格学生的平均分为________分。
20、全班有50名学生参加冬季长跑锻炼,共跑了100天,2240千米。男生平均每天跑500米,女生平均每天跑400米,则男生有________人,女生有________人。
21、在一次数学测验中,包括小明在内的5名同学的平均分为70分,其中小明得了96分,则小明以外的另5位同学的平均分为_________分。
22、学校把一批练习本平均分给五、六两个年级的学生,每人可得4本;如果只发给五年级的学生,每人可得6本;如果只发给六年级学生,每人可得_______本。
23、在一次数学竞赛中,五(1)班10名参赛学生的平均分是76分,前六名的平均分是80分,后六名的平均分是73分,那么第五名和第六名的平均分是_______分。
24、某商场每月计划销售900台电脑,在5月1日至7日黄金周期间,商场开展促销活动。但5月的销售计划增加了30%,已知黄金周期中平均每天销售了54台,则该商场在5月的后24天平均每天至少销售__________台才能完成本月的销售计划。
25、有四个数,用其中三个数的平均数,再加上另外的一个数,按这样的方法计算,分别得到:28,36,42,46,那么原来四个数的平均数是_________。
26、小永的三门功课的成绩,如果不算语文,平均分是98分;如果不算数学,平均分是93分;如果不算英语,平均分是91分。小永三门功课的平均成绩是________分。
27、6位同学数学考试的平均成绩是92.5分,他们的乘积是互不相同的整数,最高分是99分,最低分是76分,则按分数从高到低排列,位居第三的同学至少得________分。
28、老师在黑板上写了18个自然数,让同学们求平均数,要求计算结果四舍五入保留两位小数。李静同学算得的答案是17.42,老师说最后一位数字错了,其它的数字都对。则正确答案是_____________。
29、一次数学测验,小羽所在小组11位同学的平均分是82分,其中最高分98分,最低分62分,小羽得93分,还有两位同学分别是79分和88分,其余6人5人分数相同,分数各不相同的7人平均分是81.2分,小豪与别人分数都不同,小豪得分是多少?
30、A,B,C,D四数中每次选三个数的平均数,再加上另外一个数,用这种方法计算4次得到四个数,分别是85,105,73,79.问:四个数分别是多少?
31、有12000人参加歌咏比赛选拔,有200人被录取,录取者的平均成绩比未被录取者的平均成绩高36分,全体考生的平均成绩是60分,录取分数线比录取者的平均成绩低9.4分,那么录取分数线是多少分?
好了,欢迎交流,更多分享下期见。
,