欧拉公式与三角函数的推导,欧拉公式与三角函数关系

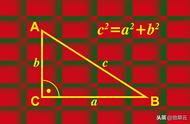
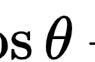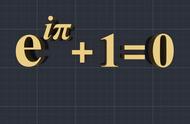那么根据函数方程，

E(2)=E(1)E(1)=e²

E(3)=E(2)E(1)=e³

........

所以E(x)=e^x 对所有整数x都是成立的。再根据函数方程

E(1/3)E(1/3)E(1/3)=E(1/2)E(1/2)=E(1)=e

又因为E(1/2)，E(1/3)都是正数，所以

E(1/2)=e^1/2

E(1/3)=e^1/3

进一步可以推导出E(x)=e^x 对所有有理数，对所有实数(取极限)都是成立的。所以E(x)是指数函数e^x 的推广。对于复数x，我们也把E(x)写成e^x。比如e^it就是：

(微分方程) (e^x )'=e^x

逐项求微分就可以得到这个微分方程：

相信不少人都知道e可以用复利的方式来理解：

假如有人借给你1万元高利贷，年化利息是100%，那么一年后结算，你要还他2万元。但是如果他半年后结算，就是(1 1/2)万，然后再借给你，半年后再结算，那就是(1 1/2)²万=2.25万。如果每四个月结算一次，那一年后就是(1 1/3)³万≈2.37万。如果把一年分成许多个，甚至无数多个时间段，不停地，连续地复利结算，那最后的结果就是极限

这个极限也是约等于2.718。也就是说最先的1万元，在一年的时间内连续复利，最后变成约等于2.718万元

另一方面，当x从0连续变到1的时候，函数e^x的值是从1增长到e，而且e^x的微分方程表明，这种增长方式也是每个时刻都以自身的值作为增长率，这和上述的复利模式是相同的。所以我们很直观地从e^x的微分方程看出