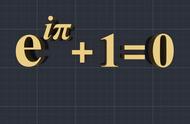共轭等式告诉我们,函数ex在一对共轭复数处取的值也是互为共轭的。
四,揭开欧拉公式的神秘面纱
我们现在重新来审视欧拉公式
(欧拉公式) eit=cost isint
这个公式的左边是一个定义在整个实数轴上的复值函数,也就是说,对于每个实数t,都对应着唯一的复数eit。我们在文章《复数——几何直观和代数运算的交响乐》中讲过,复数和平面上的点一一对应。所以如果我们把数轴看成时间直线的话,

eit就可以看作是一个质点在平面上的运动,在t 这个时刻,质点的位置是eit。
但是这个公式的右边也是一个定义在整个实数轴上的复值函数,也可以看作是一个质点在平面上的运动。我们在第一节中说过,函数 cost,sin t 分别表示(以原点为圆心的)单位圆周上,逆时针偏离(1,0)点弧长距离为t的点的横坐标和纵坐标,
也就是说,在时刻t,质点在单位圆周上走过长度为t的路程。换句话说,欧拉公式的右边代表质点绕单位圆做逆时针匀速圆周运动,速度为1。

所以,我们要说明欧拉公式的左边eit也代表质点绕单位圆做逆时针匀速圆周运动。我们先来说明为什么函数eit的值总是落在单位圆周上。根据ex的共轭等式

而根据ex的函数方程