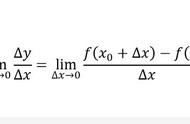当我们仅需要考虑一维情况时,比如电荷均匀分布的无限大平行板电容器之间(不包含
极板)的电场,我们知道该电场只有一个指向,场强处处相等,于是该电场满足一维拉普拉
斯方程,即

这就是说如果那边平行板电容器的负极板接地,则板间一点处的电压与该点距负极板的
距离呈线性关系。
II.散度的梯度:散度的梯度,从上面的公式中可以看到结果会比较复杂,但是它的物理意义却是很明确
的,因为从麦克斯韦方程可以看出空间某点处电场的散度是该点处的电荷密度,那么再求梯
度就是空间中电荷密度的梯度。这就好比说清水中滴入一滴红墨水,起初水面红色浓度最高,
杯底浓度最低,这样水面与杯底形成一个浓度梯度,红墨水由水面向杯底扩散,最后均匀。
在半导体中,载流子分布的不均匀会导致扩散电流。
散度的梯度这个概念其实不常用,因为计算复杂,但在后面讲用它来推导一个矢量恒等
式。
III.梯度的旋度:对于梯度的旋度,直接把(2)式代入(4)式中,有

由于势函数在空间一点的领域内往往是有二阶连续混合偏导数的,因此上式的结果为 0.所以说梯度的旋度为零,它的物理意义也是很明确的。
比如一个人从海平面爬到一座山上,无论它是从山的陡坡爬上去还是从缓坡爬上去,亦
或者坐直升机上去,重力对他所做的功总是相等的,即力场的做工只与位移有关,而与路径
无关,这样的场称为保守场,而保守场是无旋场。再比如绘有等高线的地图,如果某点只有
一个一根等高线穿过,那么该点有一个确定的相对高度。如果该点有两条或以上的等高线穿
过,则这个点处在悬崖边上,这个点处是不可微,也就没有求梯度的意义。
IV.旋度的散度:求旋度的散度也是将(4)式代入(3)式即可。若令

eq.7
则