lg计算公式,lg函数计算公式一览表

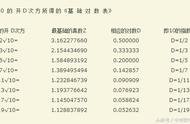
对数函数是重要的函数，自然也是高考的知识点，学习对数函数常会遇到一些难点，使解题思维陷入困境，归纳起来主要有三个方面。

难点1 底数不统一

对数的运算性质是建立在底数相同的基础上的，但实际问题中，却经常要遇到底数不相同的情况，碰到这种情形，该如何来突破呢？主要有三种处理的方法：

（1）化为指数式

对数函数与指数函数互为反函数，它们之间有着密切的关系：log_aN=b

a^b=N，因此在处理有关对数问题时，经常将对数式化为指数式来帮助解决。

（2）利用换底公式统一底数

换底公式可以将底数不同的对数通过换底把底数统一起来，然后再利用同底对数相关的性质求解。

（3）利用函数图象

函数图象可以将函数的有关性质直观地显现出来，当对数的底数不相同时，可以借助对数函数的图象直观性来理解和寻求解题的思路。

例1. 若a≠1，b≠1，a＞0，b＞0，且满足关系式log_a2=，求a，b的值。

分析：已知关系式中的底数不相同，因此可设log_a2==m，转化为指数来来解决

解：设log_a2==m，则

。

于是有

，

因为 a^m＞0,

所以