【点评】本题考查了弧长的计算公式,三角形内心的性质、三角形全等的判定与性质、圆周角定理和圆的内接四边形的性质,解题的关键是正确寻找点M的运动轨迹,属于中考选择题中的压轴题.

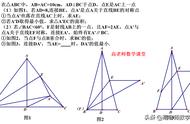
例5.(2018秋•柯桥区期中)如图,一块∠BAC为30°的直角三角板ABC的斜边AB与量角器的直径恰好重合,点E在量角器的圆弧边缘处从A到B运动,连接CE,交直径AB于点D.
(1)当点E在量角器上对应的刻度是90°时,则∠ADE的度数为_____ ;
(2)若AB=8,P为CE的中点,当点E从A到B的运动过程中,点P也随着运动,则点P所走过的路线长为______

【分析】(1)连接OE.根据∠ACE=1/2∠AOE=45°,∠ADE=∠A ∠ACE求解即可;
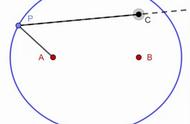
(2)连接OP,设OC的中点为O′.由PE=PC,推出OP⊥EC,推出∠OPC=90°,推出点P的运动轨迹是以OC为直径的半圆,由此即可解决问题;
【解答】(1)如图,连接OE.
∵直角三角板ABC的斜边AB与量角器的直径恰好重合,∴点A,E,B,C共圆,
∵点E对应的刻度是90°,∴∠AOE=90°,
∴∠ACE=1/2∠AOE=45°,∴∠ADE=∠A ∠ACE=75°.故答案为75°.
(2)连接OP,设OC的中点为O′.
∵PE=PC,∴OP⊥EC,∴∠OPC=90°,
∴点P的运动轨迹是以OC为直径的半圆,
∵OC=1/2AB=4,∴OO′=1/2OC=2,
∴点P的运动路径的长为π•2=2π,故答案为2π
【点评】本题考查轨迹,圆周角定理,垂径定理等知识,解题的关键是灵活运用所学知识解决问题,学会正确寻找点的运动轨迹,属于中考常考题型.

方法总结:在点的运动中,点的位置在不断变化,由此引发的是许多线段的长度和位置也随之改变,而解决数学问题则需要在这个变化过程中,寻找其变化规律以及不随点的运动而改变的性质。
中考中关于点的运动轨迹形状,通常有两种可能,一是轨迹是线段,如在坐标系中只要求出两端点的坐标就可求得路径长;二是轨迹为圆弧,此时先确定圆弧所在圆心半径,再确定圆心角就可利用弧长公式求得路径长,
,