“双减”政策中“减”的是校外补课和作业量,实则要求“增加”课堂教学的质量。 教师需要分析数学知识结构、教材编写结构和学生的认知结构,基于“本质”设计具有结构 化的学习材料,使得教学更具整体性,学生学习更具挑战性,真正用“高质”的教学落实“双 减”政策。本文通过“角的度量”一课研究的教学材料为例,为一线教师在基于数学“本质” 的结构化材料的编制和应用方面提供一些参考。
一、整体关联“找本质”
如果教师缺少整体关联的意识,对教材编排用意没有很好的理解,就难以实现基于“本 质”的教学。知识不能被割裂,需要结合学生的实际学情,并放到整个单元甚至整个领域去 分析,从而明晰概念或方法的本质。
(一)分析学生“明学情”
学生是学习的主体,是疑惑点和困难点产生的源头,也是一切教学活动的中心。放大他 们的疑惑点和困难点,找出其中的根本所在,可以为教学指明方向与路径。下面是“角的度量”一课对学生进行了分析。
1. “找”疑难
在前测过程中,让学生“试着用量角器量出一个角的大小”。在操作中,发现学生普遍存 在三种情况:第一种是无从下手,量角器在手中旋转,就是不知道怎么放;第二种是量角器 的中心点没有与角的顶点重合;第三种是量角器上的内外圈数据混淆严重,部分知道的也是 通过记忆方法,并不知道其中的道理。
2. “揪”问题
分析学生的实际学情可以利用以下步骤进行,从学生的具体错误现象进行成因分析,教 师还要站在执教者的角度,对学生的成因分析进行高度概括,用本质问题加以阐述,也就是 学生学习要解决的最主要的问题。具体分析见下图:

(二)拓宽挖深“解本质”
1.放宽领域分析教材
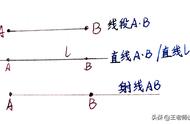
纵观小学阶段,角的认识分布在两个学段。二年级上册初步认识角,四年级上册学习角 的度量,教材遵循学生的认知规律,从定性和定量两个层次让学生理解角的意义。这两次认 识虽然时间是分裂开来的,但内容是统一的。
二年级第一次从实物中抽象出角,学生难以排 开边的长度来关注角的大小。到四年级重新定义角的含义,学生才真正能化解“线的无限、 不可量化”和“角的度数的有限、可量化”之间的矛盾。而“角的度量”又进一步让学生用 标准的单位“1 度”来测量,从粗略的感知到细致的刻画,这样一来,学生才能真正理解“一 个角的两边无论怎么延长或缩短,都表示同一个角”。
测量角与测量长度、面积等其他的量既 是属于同一个“度量”体系,又有其特殊之处,比如“内外圈”两圈数据、角的顶点要与量 角器的中心点重合等等。“角的度量”一课是角认识的关键课,为后续“角的分类”、“图形的 再认识”做好铺垫。
2.深入分析抓住本质
要知道教学的本质,可以从学生实际学情的“本质问题”出发,将问题细分,最终聚焦 在其中的“核心问题”上,挖出教学的本质。

在平时的教学中,很多教师会过分强调量角的方法,“点对点,边对边,角朝左,读外圈, 角朝右,读内圈”,忽略了量角的本质意义。从以上分析可知,有效的教学应让学生明确“量 角”即“找等角”,由此才会明白用量角器上标有刻度的标准角来与被测角的顶点和边分别互 相重合,也就相等了。内外圈数据只是方便读数而已,不是教学的本质,内圈和外圈分别的 对应关系是随着量的角张开两边所在位置而定的,理解了量角即找等角后,自然而然会明白。
二、基于本质“改材料”
理解教学的本质意义后,关键是需要一副好的结构化材料,否则是难以实现这样的教学 目标的。材料的选择非常灵活,要牢牢紧扣教学的“本质”。在实践中不断尝试、改进,使它 更有利于学生的学习。
(一)初试材料,关注整体教学
1. 学习材料

反馈交流过程:
(1)你们同意哪些量角的方法? 生:同意①②③,不同意④。(有些学生不同意③) (2)为什么?他们分别是怎么量角的? 生:量角器的中心点与角的顶点对齐再量。 (3)③行吗?为什么? 生:110°-60°=50°
(3)除了计算,你还有什么方法知道是 50°? 生:数有几个大格,5 个大格是 50°。
2.材料分析
以上教学片段中,四种有代表性的材料看似比较有结构,错例④号让学生明晰量角的方 法,三种不同的正例①②③号方法凸显量角的本质,自己认为非常满意。为了突出这点,极 力让学生关注被测角与量角器中角的关系。
想通过“为什么量出来都是 50 度?”“50 度还能 怎么看出来?”等问题把学生的关注点从“数据”转移到“刻度”上来,也就是有几个 10° 或者有几个 1°角。教学中,在“观察数据计算度数”和“数有几个标准角”中,学生喜欢 选择前者,由于便捷。
如果强制学生关注有几个标准角,学生切身的感受也不深刻。这样的 材料看似具有结构化,实则没有基于学生的实际情况进行探究量角的本质。如何才能让学生 主动关注刻度角,而不受数据的影响呢?如何让学生明白“量角”即“找等角”呢?这就需要排除数据的干扰,让学生完全关注刻度角。
(二)再试材料,关注本质教学
1.学具主材料的确定
有一种半透明的雪梨纸,可以直接打印需要的量角器。基于此,将量角器上的数据剔除, 把完整量角器变成了只有大格的简易量角器,如左下图所示。 用这样的量角器去量角,在不给刻度的情况下,学生能知道被测角的 度数吗?学生已经知道了直角是 90°,把 90°平均分成 9 份,不难知道每 个大格是 10°。
这样的量角器能够直接让学生只关注刻度,突出量角即找 等角,度数就是数几个十度角的累加。但也有一定的局限性,只能测量整十度的角,不是整 十度的角是不能测量出比较精确的结果的。这些问题需要设计一个大任务,具有一定的挑战 性和趣味性,更能激发学生的学习热情。
2.教学主环节的确定
小组成员在县教研员杨老师的带领下,对“角的度量”这一节课进行了重构。主要环节 如下:
环节一: 引入量角 (不给学生度数,实际∠1=50°,∠2=47°) 比一比∠1 和 ∠2 谁大谁小