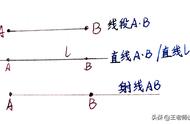
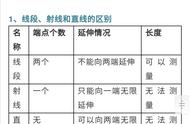
随着教学的推进,学生的感知渐渐深入,清楚地意识到“量角”即“找等角”。不完 ① ② 整的量角器,能让学生的学习真正可见。
4.量角的“精细化”过程直导“量角器”的产生。
一切精准的单位都是实际测量的需要,量角也不例外。从测量整十度的∠1 到测量不是 整十度的∠2,是测量标准改变的又一次飞跃。当三号“十度”标准的量角器不能比较精确测 量时,学生想到了再平均分成两份、五份、十份等,需要更小的测量单位。有的说标准改成 “5°”,有的说“2°”,还有的说“1°”。
学生说的更小的标准角其实都可以在特定的时候 使用。在这样的活动中,学生显然已经感知到测量标准的选择是根据实际需要的结果。在多 媒体课件的演示过程中,呈现学生的思考,最终以“1°”标准度量出∠2 的度数是 47°,4 个 10°和 7 个 1°(如下图所示)。将计数单位的“十”变成“一”,10 个“一”度是 1 个“十” 度,完全符合人类习惯运用“十进制”计数的特点。量角器的形成过程可以用以下图示进行 表示:

“是否可以用∠1 测量∠2?那∠2 测量∠1 呢?”本身两个不相*角,肯定不行。这 样的问题提出,出乎意料的是学生竟然也能想到了将∠1 平均分成 50 份,每份得到标准角 “1°”,这样一来,∠2 就能在∠1 中找到 47°的角与它重合。但由于∠2 小于∠1,用∠2 来测∠1 不够大,需要再测一次多余部分。
到这里,学生似乎头脑中已经形成一个观念:任 意一个角都能成为一个量角器,只要将它平均分成更小的标准单位。到这里,量角器已经在 学生的头脑中慢慢形成了,最后展示我们经常使用的工具——量角器,内外圈数据只是为了 方便我们读数,知道测量的结果。(二)“说”材料,“理”教学
1.“缺损”材料助推本质教学。
*后的这节课教学效果非常不错,学生乐于参与其中。*后的教学材料是真正基于 学生现实的学情,利用不完整的量角器,特别是设计了“缺少数据”和“破损”的量角器这 些材料,能够将“量角器为什么能量角”这个问题给解决了。在小学数学教学中,关于度量 的知识还有很多,同样可以借助类似“缺损”的工具编制材料进行应用,利用这样的材料能 让学生在思辨中理解数学的本质。
2.“逻辑”问题促进有效学习。
基于本质的材料需要有逻辑的问题进行串联,就是要把材料中知识的内在逻辑与学生的 认知逻辑统一起来,通过有逻辑的一系列问题揭示教学内容的数学本质和知识间的结构关系。 从而,促进学生对概念的核心问题、思想方法等有一个整体理解,达到学生有效的学习。
,