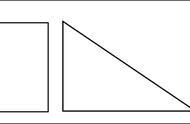
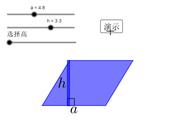
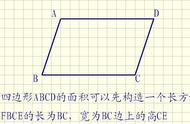
引导学生边演示边说明,交流汇报小组探究情况。
师:把平行四边形沿着高剪拼变成长方形,长方形的面积是28 cm2 ,所以平行四 边形的面积就是28cm2 ,为什么?
学生观察思考,能想到:因为剪拼的都是这一块,它们的面积是相等的。
师:看来整个图形在剪拼过程中没有增加,也没有减少,它们的面积是相等的,长 方形的面积是28 cm2 ,平行四边形的面积也就是28 cm2 ,这个猜想又一次得到了验证。
师:那为什么要把平行四边形变成长方形?
学生能想到:长方形的面积我们学过,这样能简单地求出平行四边形的面积。
师:刚才我们通过不同的方法验证了这个猜想是正确的,而其他的猜想不对。虽然 这种猜想不对,但是同学们却敢于猜想,牛顿说过“只有大胆的猜想,才有伟大的发现 和发明”。当然,光猜想还是不够的,还需要勇于实践验证猜想。
师:好,我们继续,拼成的长方形与原来的平行四边形之间有怎样的关系?
生:我们沿着平行四边形的高剪下,平移拼接成一个长方形,拼成后的长方形面积 与原来的平行四边形面积相等,拼成后的长方形的长就是平行四边形的底,拼成后的长 方形的宽就是平行四边形的高。长方形的面积和平行四边形的面积相等。
师:根据大家的发现,说说平行四边形的面积怎样计算?
学生能结合实践经验想到:长方形的面积等于长X宽,那么平行四边形的面积等于 底X咼。
师:你能用字母表示平行四边形的面积公式吗?
学生能结合已有的知识经验,想到:S=ah
师:这个公式中S、a、h各表示什么?
学生能想到:S表示平行四边形的面积;a表示平行四边形的底;h表示平行四边 形这条底上的高。
师:那我们只要知道了平行四边形的底和高,我们就能求出平行四边形的面积。平 行四边形卡片底是7cm ,高是4cm ,面积就是28平方厘米,验证猜想正确。长方形的 面积我们学过,这是旧知,平行四边形的面积是新知,把新知转化成旧知的方法叫做'转 化”。转化是我们在数学学习中经常会用到的方法。好,回到我们的情境问题,现在你 能解决情境图的问题了吗?
学生口头列式,计算玻璃的面积:1.2x0.7=0.84 (平方米),这块玻璃的面积是 0.84平方米。
师:回顾刚才我们探究平行四边形面积公式的过程,我们把平行四边形的面积转化 成长方形的面积,把新知转化成旧知;然后又寻找两种图形间的联系;最后推导出平行 四边形的面积公式。整个过程的进行模式,有助于我们以后研究其他图形的面积,同学 们在之后的学习中也可以采用这种方法进行研究,解决问题。
师:刚才我们用数方格以及把平行四边形沿着高剪下一部分,平移补充到另一部分, 拼变成长方形的过程,我们采用的方法叫割补法,也叫“以盈补虚”。早在魏晋时期,伟 大数学家刘徽在《九章算术》中就提出“以盈补虚,出入相补”的方法。这种方法经常用 来解决图形的面积、体积计算问题。《九章算术》第一章“方田章”中主要论述了平面几何图形面积的计算方法,从这一章,我们可以发现古代平面图形面积计算方法和现代的计 算公式相同,而这些计算方法,我们的祖先早在两千多年前就已经掌握了。看完之后, 你有什么想说的?
课下,同学们可以搜集相关的资料,补充数学文化。
(三)、应用公式,解决问题
师:这节课的知识,同学们掌握的怎样呢?老师带来了几个问题,请同学们拿出练 习本,老师来考考大家。
1、
计算下面平行四边形的面积。