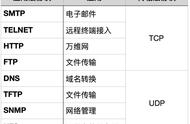
在表1中,我们计算了短条数从10条到20 000条时的短条总面积。条数(N)为20 000时,每条短条的宽度Δx是半径的1/10 000,只有0.000 1 cm。
我们从表1的结果中可以发现,条数为10时,总面积是2.637 049,这个数值和3.14…迥然不同;当条数为20 000时,总面积则成了3.141 391。怎么样?是不是可以切实感受到,当短条的条数增加时,短条的总面积会逐渐接近3.141 592 6…=π。
另外,虽然短条宽度为0.000 1 cm已经是纤细至极,但在分割图形时并不算是“精细”的尺度。实际计算积分时,会使用比0.000 1 cm更精细、更接近0的尺度。
作者简介

神永正博(Kunihiko Kodaira) 1967年出生于东京,理学博士,日本东北学院大学教授。曾在京都大学研究生院理学研究所(数学方向)进行博士后期课程学习。主要研究方向为解析学(作为量子力学基础方程式的薛定谔方程)以及密码理论。主要著作有《看穿谎言的统计学》《数学思考法》,另外审阅翻译的著作有《漫画统计学入门》等。

微积分的本质在于方法。简单说,如果抓住思考的“要领”,那么就能轻而易举地理解复杂算式。相反,如果不能掌握思考要领,直接从计算技术入手的话,微积分的学习便如同咀嚼沙子一般变成了苦涩的修行。
——神永正博
目录及更多
简单微积分
学校未教过的超简易入门技巧
向上滑动阅览简介及目录
本书为微积分入门科普读物,书中以微积分的思考方法为核心,以生活例子通俗讲解了微积分的基本原理、公式推导以及实际应用意义,解答了微积分初学者遭遇的常见困惑。本书讲解循序渐进、生动亲切,没有烦琐计算、干涩理论,是一本只需轻松阅读便可以理解微积分原理的入门书。
目录:
第 1章 积分是什么 1
积分的存在意义 2
积分应用的基础 2
所有图形都与长方形相通 5
近似的方法 8
和变为了积分 13
何为“接近精确值” 18
两个思想实验 20
椭圆的面积 20
地球的体积 25
切口的秘密 32
卡瓦列利原理 32
三分之一的原理 37
圆锥的体积 45
球的体积 48
球的表面积 54
感觉和逻辑 59
初中入学考试中的积分 59
像小学生那样求圆环体体积 67
把甜甜圈变成蛇的方法 69
帕普斯-古尔丁定理 73
第 2章 微分是什么 77
微分存在的意义 78
分析钻石的价格 78
“亮出指数”的理由 86
乘积的微分公式 94
从未知到已知 97
商的微分公式 100
再次扩展幂函数的微分公式 102
丰富多彩的函数世界 105
山峰和山谷 105
了解切线 109
根据单调性表画函数图像 113
最大值和最小值、极大值和极小值 117
手绘函数图像的意义 119
存在休息平台的函数 121
有预谋地使用微分 128
理想的冰激凌蛋卷筒 128
忽略与不可忽略的界线 138
第3章 探寻微积分的可能性 141
1800年后的真相 142
反军队式学习法 142
伟大的发现会成为未来的常识 144
基本定理的使用方法 152
填坑 160
自然常数从何而来 160
无限接近于最确的值 164
关键在于根号 166
转换思路能行得通吗 169
指数函数出现了 175
让关系更清晰 178
唯一个微分后不会发生变化的函数 181
弯曲也没问题 184
测量曲线的长度 184
简洁的悬链线公式 187
验证项链的长度 194
微积分的真身 199
微分的可能性 199
微分相关的冒险 202
近似和忽略 205
后记 207
尾注 209
好玩的数学
*mathfun
↑
好玩的数学以数学学习为主题,以传播数学文化为己任,以激发学习者学习数学的兴趣为目标,分享有用的数学知识、有趣的数学故事、传奇的数学人物等,为你展现一个有趣、好玩、丰富多彩的数学世界。

↓
点阅读原文购买《简单微积分》。
,