托里拆利大气压实验
而且,托里拆利还是著名科学家伽利略的学生,也是当时最受尊敬的数学家,

伽利略
这个问题当然也难不倒托里拆利,他很快作出了回答并证明:
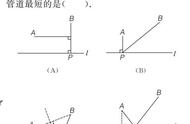
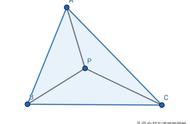
当点P满足∠APB=∠BPC=∠APC=120°时,AP BP CP最小。

费马接到回信后很开心,毕竟托里拆利可是非常有名的数学家,他自己当然知道答案,是为了挑战托里拆利才故意向他请教的。
因此,这个点也叫费马点或托里拆利点。
费马点就是到三角形的三个顶点的距离之和最小的点.
证明方法很简单:

首先任取一个顶点A,然后以A点为旋转中心,将△APC 逆时针旋转60度到△AP'C'位置。
这样就通过旋转构造了一对全等三角形和一个等边△APP'。
易知PC=P’C’,AP=AP’=PP’,所以PA PB PC=PP’ PB P’C’,
显然当B、P、P’、C’四点共线时,距离之和最短。