当B、P、P'共线时,∠APB=120°,当P、P'、C'共线时,∠AP'C'=∠APC=120°,
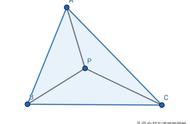
所以P点应该对三个顶点的张角都为120°,这就是费马点的位置。
我们也可以用一个动图来演示:

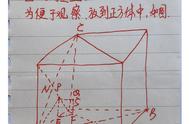
证明方法是利用了旋转变换的思想,把三条线段 PA, PB, PC拼接起来,成为一条折线,再利用“两点之间,线段最短”的线段公理,化折为直,就能确定 PA PB PC 的最小值了。
本质还是——化折为直。

怎么样,同学们,你学废了吗?
,当B、P、P'共线时,∠APB=120°,当P、P'、C'共线时,∠AP'C'=∠APC=120°,
所以P点应该对三个顶点的张角都为120°,这就是费马点的位置。
我们也可以用一个动图来演示:

证明方法是利用了旋转变换的思想,把三条线段 PA, PB, PC拼接起来,成为一条折线,再利用“两点之间,线段最短”的线段公理,化折为直,就能确定 PA PB PC 的最小值了。
本质还是——化折为直。

怎么样,同学们,你学废了吗?
,












Copyright © 2018 - 2021 www.yd166.com., All Rights Reserved.