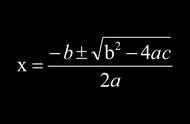一元二次方程求根公式谁发现的,一元二次方程根的求根公式

四次方程的费拉里方法

数学家们发现，解一般四次方程总依赖于一个三次方程，是否可以将一般五次方程的解归结为解四次方程呢？欧拉大约在1750年进行尝试，但结果失败了。法国的拉格朗日约于1770年完成《关于代数方程解的思考》一文，明确指出“不可能用根式解四次以上方程的”。他的学生鲁菲尼也证明了这样一个事实：一般五次或五次以上的方程不可能用方程系数的根式表示。后来挪威数学家阿贝尔也独立证明了一般五次方程不可能存在求根公式，但什么样的特殊方程能够用根式表示的判断没有解决。不过，这个问题被法国数学家伽罗瓦解决了。

伽罗瓦

探索数学的道路是无止无境的，求解方程只是数学的一小步，但没有这一小步，人类未来将迈不出一大步。