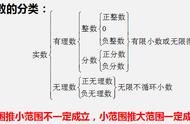
图3:看起来不特别美味的甜甜圈
为什么球体不是甜甜圈?
现在,我们知道了如何判断两个对象在拓扑中的一致性,现在我们来看一下如何判断其在拓扑中的差异性。拓扑空间具有许多可以区分它们的不同属性。对于三维对象,例如球体和甜甜圈,我们可以用来区分二者的主要是它们具有的孔数。如果一个对象比另一个对象具有更多的孔,则二者在拓扑上是不同的。这是因为它们违反了我们先前建立的拉伸橡皮泥的规则。要造出一个孔,我们要么在橡皮泥上撕出一个洞,要么将橡皮泥拉伸成一个甜甜圈形状,然后将两端合并在一起。

图4:我们可以将橡皮泥球塑造成甜甜圈形状,但是在不违反规则的情况下,边线不能融合在一起。当我们将其弯曲成甜甜圈时,通心粉形状的两个圆形面仍然存在。
在拓扑上区分三维对象的另一种常用方法是,想象在三维对象上面行走。例如,在球体上行走。假设你从某个点开始,一直绕着球体上的一个大圆圈行走,当你再次到达同一点后,可以沿任一方向旋转90度,然后绕着另一个大圆圈走。在绕球的第二圈中,你将穿越第一条路径。无论你在球面上的哪一点上执行此操作,都会发生这种情况。

图5:具有两条相交路径的球体
在与球体拓扑等价的任何三维对象上也会发生这种现象。但是,在某些拓扑上与球体不等价的对象上,有方法可以做到这一点而不穿越第一条路径,你可以在甜甜圈上看到这个现象。

图6:如果我们从蓝色和绿色路径相交的地方开始,然后沿着绿色路径行走,这条路径跟我们已经走过的地方不相交。
对于拓扑等价的对象,他们的许多拓扑性质都是相同的;对于拓扑不等价的对象,这些拓扑性质则不一定相同。这些拓扑性质,就是用于确定两个对象拓扑等价与否的重要工具。
其他的拓扑对象
到目前为止,我们仅讨论了可以在3维中可视化的拓扑空间,但拓扑的一个优势是,它允许我们使用同样的方法轻松地描述4、5或更高维中存在的对象。
此类拓扑结构中经常出场的是克莱因瓶: