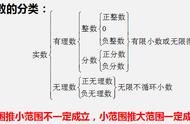
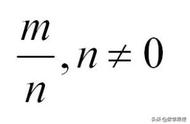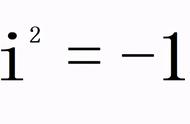图7:三维空间中克莱因瓶的表示 | youtube:Numberphile
严格来说,我们实际上无法在三维空间中观察到真正的克莱因瓶,但是通过允许其自身交叉,我们可以对它的性质有所了解。在四维空间中,该对象实际上并不与自身交叉。很难想象的是,它会在第四维度弯曲以重新连接到自身。克莱因瓶看起来像有内外两侧,但是你可以从一个特定点沿一条连续的路径走,你将经过克莱因瓶的“外部”和“内部”,最后回到原始点,这说明克莱因瓶的3D表示在拓扑上是同一个面。因此,克莱因瓶没有容积。
但是,关于克莱因瓶上的路径的一个有趣的事情是,如果沿着上述路径行走,当你返回到原始位置时,你实际上将成为自己的镜像。这是与克莱因瓶在拓扑上等效(或同胚)的对象的拓扑属性。显然,克莱因瓶对球体或甜甜圈不是同胚的,因为无论我们在球体或甜甜圈上行走的方式如何,当我们回到起点时,我们都不会成为自己的镜像。如果对象具有成为自己镜像的这种属性,则将它们称为不可定向的。克莱因瓶不可定向,球形和甜甜圈可定向。另一个著名的不可定向表面是莫比乌斯带,这个很容易用纸条制作,网上也有很多教程。

当螃蟹在莫比乌斯带上行走并返回其原始位置时,它就是其自身的镜像。资料来源:Wikimedia Commons
尽管莫比乌斯带不可定向,但它在拓扑结构上不等同于克莱因瓶,而且其结构是一个整体。虽然可以通过将两个莫比乌斯条的边缘粘合在一起来构造克莱因瓶,但实际上在三维空间中这样做是不可能的(你可以尝试)。
用一张纸构造一个甜甜圈
研究在三维空间中难以可视化的对象(例如克莱因瓶)的拓扑的一种更实用的方法是考虑其粘合图,粘合图通过拉伸和粘合2D形状的边缘的方式,来指导我们如何构造具有特定拓扑的对象。
在考虑复杂形状的粘合图之前,首先考虑一个更简单形状的粘合图,甜甜圈:
图7:甜甜圈的粘贴图
我们假设图中的正方形是用橡皮泥制成的,然后想象一下拉伸正方形让对侧的边缘附着在一起或粘贴起来。当我们将这些边缘粘合在一起时,我们需要箭头指向同一方向。因此,我们将上图扩展如下:

图8:如何从其粘合图构造甜甜圈
下一个图类似于图 7,除了两个红色箭头现在处于相反的方向。这意味着我们需要扭曲对象,以便在将边缘胶合在一起之前,箭头指向同一方向:
图9 :更复杂的粘合图
上图粘合图中的第一步是拉伸正方形,使两条蓝线相交,然后我们构造一个圆柱体,就像构建甜甜圈的第一步一样。甜甜圈粘合的红色箭头指向相同的方向,而现在,这两个红色箭头则指向相反的方向。这意味着我们必须以某种方式扭转圆柱体的一端,以使箭头在将它们胶合在一起之前指向相同的方向。你可能会想到,这在物理上是不可能的。因此,由该粘合图产生的表面在物理上也是不可能的。但是实际上,这是我们已经见过的物理上不可能的表面,克莱因瓶!

Source:Fouriest Serieson tumblr
粘合图是查看对象是否可定向的简单方法。我们可以想象在粘合图上行走与在“吃豆人”中的原理类似,当吃豆人到达世界的一侧时,它可以从另一侧出来。如果我们想象吃豆人在粘合图上移动,当它进入一侧时,它将从同一颜色的另一侧冒出来,而箭头确定了它前进的方向。
假设吃豆人进入圆环粘合图的右侧,那么它将从左侧出现。这就是正常“吃豆人”世界的拓扑工作方式。