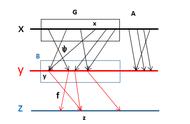
直观上看,一个对数函数就一定对应着一个指数函数,那我们已经有了指数函数,为什么还要创造一个对数函数呢?其实我们可以这样看,对数函数和指数函数单调性是一致的,并且十分相关,这就为解决计算提供了简便的方法。举个栗子:地球到太阳的距离是1.519*10^8km,转换成自然对数值为18.839,一下子就将数字减小了不少,减小的意义在于大数计算时大大压缩了计算时间,提高了效率,特别的,对数函数特有的计算规则,可以将乘除转化成加减,这又大大提高了效率,一句话,对数函数在对付大数字时,就像一个压缩器,把埃菲尔铁塔压缩成桌子上的模型,但却没有损失一点信息。
Wolframalpha小贴士:对数函数的底数可以直接log跟上数字即可,如以2为底的对数函数,可以输入y=log2(x),特别的自然对数,可以输入y=ln(x)
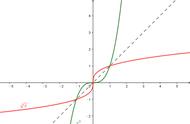
(4)幂函数:幂函数的起源已经不可考,但是我们可以猜测,其一定是来源于实际情况,并且进行了扩展。我们需要数出一排x人,共x列,共有多少人,就是x的二次幂(也就是平方)。我们需要计算一间长宽高均是x米的房子有多少体积,就是x的三次幂(也就是立方)。这样我们只需要知道x,就有一个对应的幂结果,这也就成了幂函数。和指数函数一样,底数不同,单调性和增减幅度差别很大,如图:

这里只画出了第一象限
Wolframalpha小贴士:对需要同时画出很多函数图形的情况,可以使用“{}”,比如上图就是用了如下命令:plot {x^2,x^5,x^(1/2),x^(1/5),x^(-1/2),x^-2},相当于省去了很多个and。
(5)三角函数:这是中学说过n遍的东西,它其实就是为了便于进行角度与边长之间的计算,举个栗子:太阳光以与地平呈30度角照射你,你身高1.8米,影子长就是1.8*cot30或者1.8*cot(Pi/6)。三角函数主要的就是四个:sinx、cosx、tanx,cotx。其实只需要知道一个,就能够推出其他三个,但为什么还要搞出这另外三个呢?我们可以这样理解,乘法不就是优化了的加法吗?所以一切就是为了方便再方便而已。对于三角函数,强烈推荐使用单位圆辅助记忆及公式间推导。单位圆我会另作一篇进行介绍。三角函数讲个历史小故事:我们现在都叫的勾股定理或者毕达哥拉斯定理,其实早在西周就有个叫商高的人发现了,比毕达哥拉斯整整早了500年。

(6)反三角函数:和指数函数与对数函数一样,反三角函数就是三角函数的反函数。主要也是四个:arcsinx、arccosx、arctanx、arccotx。可以这样理解,三角函数是为了已知角度求边长,反三角函数就是为了已知三角函数值求角度,前面的arc古代意思为弓弦,也就引申为弧度。需要什么,就创造什么,这就是历史的规律。

可以看到,在WA中,arcsinx就是被解析成sinx的反函数
认识了这六个基本初等函数,下一篇就要进行下升华,从这六个基本初等函数变化出简单初等函数和初等函数,而这些函数特有的优质特性,也是微积分利用到的,另外插一句,微积分之所以看重这六类基本初等函数,就是因为现实世界的抽象大都汇聚于此。
我是WA小刀,如果觉得我写的还行,请关注支持下,也鼓励下我不断前行。
,