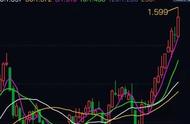
图三 高斯定理公式二
结合上面材料,下面就个人理解,对散度进行如下解释:按散度解释一,散度表示场中一点处通量对体积的变化率。那么,如何理解这句话呢?现在,我们假设,图一散度中的球体,外面包裹了一块同样球形的膜,那么,这层膜就包围了这个球体所发出的所有电力线(电通量),我们假设电力线的数目是10000根,而此时这层膜的体积等于1,那么电通量体密度就是10000;再假设这层膜现在扩大到原来体积的10倍( 意味着单位体积元离开带电球体的距离增加),根据高斯定理公式一,这层膜包围的电通量不会改变,一直都等于10000,那么此时电通量体密度就是1000;那么,这层膜的体积在由1变到10的过程中,电通量体密度就由10000变到了1000,电通量密度随体积变大10倍而改变的比例是(10000-1000)/10000=90%;再假设这层膜的体积由10变到100,经过同样分析,电通量密度随体积变大10倍而改变的比例还是
(1000-100)/1000=90%。

太阳光
这一结果和我们对于太阳光的感觉是一致的:即太阳光的强弱变化是随着离开太阳距离的变化所做的一种匀速的,等比例的变化过程。对照图三,这个公式和前面的分析结果是一致的,也就是说,在带电球体的外侧,散度即电通量体密度的变化率是相同的,而这句话的真正含义就是:电场散度即电场中任一点处通量对体积的变化率是指:这一点电通量体密度的变化,是和该点距离带电球体的远近(相对应的那层球形膜的体积)成比例变化的,而这个比例在带电球体外的任何一点都是固定的,即单位体积内包围的电力线的根数是和这个体积元与带电球体的距离成比例增加或减少的。
假设我们面前有一个灯泡,现在我们匀速倒退离开这个灯泡,我们会感觉到,灯泡的亮度是逐渐变暗的,也就是和我们离开的距离成比例变暗的。
有了上面的分析结果,我们再看看上面的散度解释二:散度可理解为通过包围单位体积闭合面的通量。
那么,这样的表述是有问题的,至少是不严谨的,可以考虑更改为:散度可理解为通过包围单位体积闭合面的通量的变化率。
再看百度百科对散度有一个描述:散度是描述空气从周围汇合到某一处或从某一处流散开来程度的量。水平散度是气体在单位时间内水平面积的变化率。如果面积增大,散度取正值,为水平辐散;如果面积缩小,散度取负值,为水平辐合。三维空间的散度表示任意气块在单位时间内其单位体积的变化率。
其中最后一句的含义和本文分析的结果是相通的。
前面分析已经指出,电场散度即电场中任一点处通量对体积的变化率。
由此我们猜想,那个变化率应该就是

里面的那个p。为了证明这个猜想,现假设包围体电荷q的球膜的体积由V变为了V0,由于q始终不变,所以V0越大,单位体积元中通过的电力线数目越少,两者是反比关系,此时单位体积元中的电力线数目改变为Y:
Y=pV/V0,
由于p就是最大的单位体积里的电力线密度,所以单位体积里的电力线数目只能在这个基础上去减少。这里V是常量,但V0是变量,因此V/V0是变量,这里用X代替,那么,
Y=pX
这个方程就表示了体电荷q之外某一点所在的单位体积内包含的电力线数目随这一点离开体电荷q的距离(即变化的体积V0)变化而变化的方程。
再按照图二的解释,散度表示的是电场中一点处通量对体积的变化率,而方程Y=pX表示的则是电场中一点处通量对体积的变化关系,因此将Y对X求导,则dY/dX=p,而dY/dX表示的正是电场中一点处通量对体积的变化率,即散度。由此我们知道了,

这个符号原来就是方程Y=pX的斜率。这就从根本上解释了