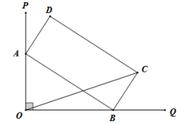
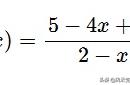分析 作P关于OA,OB的对称点C,D.连结OC,OD,则当M,N是CD与OA,OB的交点时,△PMN的周长最短,最短的值是CD的长.根据对称的性质可以证得,△COD是等腰直角三角形,据此即可求解.
例2 : 如图8,菱形ABCD中AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK QK的最小值是多少?


分析 根据轴对称确定最短路线问题,作点P关于BD的对称点P′,连结P′Q与BD的交点即为所求的点K.根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK QK的最小值,然后求解即可.
,