简单说:就是找出一个比原式小的式子和一个比原式大的式子证明他们俩的极限相同且为a,则原式极限也为 a。
1.5.2 单调有界准则
单调增加(减少)有上(下)界的数列必定收敛。
在运用上面两条去求函数的极限的时候尤其需要注意以下关键点。一是要用单调有界定理证明收敛,然后再求极限值。二是应用夹逼定理的关键是找出极限相同的函数,并且要满足极限是趋于同一方向,从而证明或求得函数的极限值。
单调有界定理:单调有界数列必收敛(有极限)。具体的说:
(1)若数列 {Xn} 递增且有上界,则:

(2)若数列 {Xn} 递减且有下界,则:

1.5.3 柯西收敛准则
数列 {Xn} 收敛的充分必要条件是:对于任意给定的正数 ε ,总存在正整数 N,使得当 m>N,n>N时,且 m≠n,有 |Xm - Xn| < ε。我们把满足该条件的 {Xn} 称为柯西序列,那么上述定理可以表述为:数列{Xn}收敛,当且仅当它是一个柯西序列。
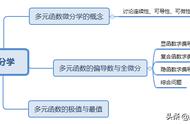
1.6 课程中的PPT