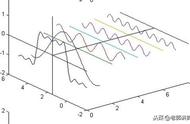
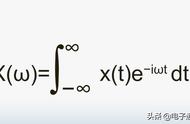傅里叶变换可以让我们从一个复杂的波形里面,把构成这个波的单个正弦波分离出来。在这个例子中,你几乎可以通过“脑补”完成这一操作。
为什么?事实证明,现实世界中的许多事物间的互相交互,都是基于正弦波。我们通常将这种波的快慢的性质,称为波的频率。
最明显的例子就是声音 —— 当我们听到声音时,我们听不到那条波浪线,但我们听到构成声音的正弦波的不同频率。
能够在计算机上区分这两个音调,我们就可以了解一个人实际可以听到的内容。我们可以理解声音的高低,或弄清楚这个波包含了什么音符。
一些波看起来不像由正弦波构成,我们也可以用这个分解的过程来进行分析。
我们来看看这个家伙吧。这个波称为方波。

虽然看起来不太可能,但它确实也可以分解成正弦波。

这次我们需要很多 —— 理论上是无限多的正弦波来完美地表达一个方波。随着我们加入越来越多的正弦波,叠加出的波形就越来越接近方波。
在视觉上,你会注意到前几个正弦波的叠加可以在结果中产生最大差异。滑块滑到一半时,就有一些方波的样子了,但它看起来摇摆不定。加上更多小的正弦波,组合出的波形看起来就平坦了。
当播放这个波形时,你会发现使用的正弦波少时,声音听起来更低沉一些。这是因为我们把高频率的成分去掉了。
这一过程可以用来处理任何有周期的波。试一试,画一个你喜欢的波形吧。

随便画一个波形都能用多个正弦波表示
随便画一个波形都能用多个正弦波表示
移动滑块来观察,正弦波加得越多,组合出的波形越接近你画的原始波形。
和上一个方波类似,除了有些额外的摆动之外,滑块移动到中间位置,生成的波形就很接近你画的了。
我们可以利用这个事实:使用傅里叶变换,我们可以把音频中最重要的成分表达出来,并且得到和原始声音非常接近的波形。
在计算机中,波形以一系列数据点的形式来存储。