物体浸没(取出)后液面上升(下降)问题,是小学数学中的一种典型考题。
物体浸没分两种情况
①完全浸没:即物体被液体完全淹没,液面上升部分的体积=被淹没物体的体积,所以液面上升的高度=浸没物体的体积÷该容器的底面积。
分析:
例1、将一个棱长为4厘米的正方体铁块,完全放入一个底面积为20平方厘米,高10厘米,水深4.5厘米的圆柱形容器中,那么水面高度上升多少厘米?
分析:容器中水面的高度大于小正方体铁块的高度,铁块完全浸入水中,此时容器中液体所上升部分的体积就等于浸入铁块的体积,液面上升的高度=铁块的体积÷容器的底面积。
解:4×4×4÷20=3.2厘米
答:水面高度上升3.2厘米。
同样的,如果将一个被浸没的物体取出,液面会下降,液面下降部分的体积=被浸没物体的体积,液面下降的高度=被浸没物体的体积÷容器的底面积。
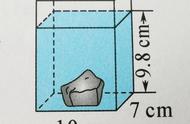
例2、一个长方体容器,从里面量长60厘米,宽40厘米,里面水深20厘米,现将一块长50厘米、宽30厘米的长方体石头完全浸入水中,这时水面上升到25厘米,求这块石头高是多少厘米。
分析:水面下降部分的体积=浸没石头的体积,石头的高=石头的体积(即水面下降部分的体积÷石头的底面积)。
解:60×40×(25-20)÷(50×30)
=8厘米
答:这块石头的高为8厘米。
②部分浸没:即物体没有被液面所淹没,仅有部分在液面以下,还有一部分在液面以上。
例、在一个长10厘米,宽为8厘米,高为20厘米的长方体容器中,里面水深9厘米,将一个长6厘米,宽为5厘米,高为16厘米的铁块竖直放入水中,使底面与容器底面接触,这时水深为多少厘米?
分析:解决这个问题之前,需要先判断一下这个铁块是完全浸入水中还是部分浸没水中。
假设完全浸入,铁块的体积为6×5×16=480立方厘米,水面上升的高度为480÷10÷8=6厘米,此时液面的高度为9+6=15厘米,小于铁块的高度,所以该铁块部分浸入水中。
解:10×8=80平方厘米
6×5=30平方厘米
设水深为x厘米,由题意得
80(x-9)=30x
8x-72=3x
x=14.4厘米
答:此时水深为14.4厘米。
[练一练]
1、在一个长20厘米、宽16厘米的玻璃杯中放入一块棱长8厘米的正方体铁块,这时水深15厘米,如果把这个正方体铁块从杯中取出,杯中的水深多少厘米?
2、一个长方体容器,其底面是边长为50厘米的正方形,在这个长方体容器里放入一根横截面为10厘米正方形、高1米的长方体铁棒,这时该长方体容器中的水深0.5米,如果将该长方体铁棒完全拿出,那么水面会下降多少厘米?若现在把铁棒竖直向上轻轻的提离长方体容器底部30厘米,那么露在空气中被浸湿的部分长多少厘米?
,