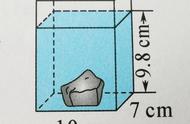
人教版五年级学生开始接触长方体的体积和表面积,铁块入水类型的题目是这个系列典型的应用题。做这类题需要把握一个小小的常识,即:

铁块入水后,占据了部分水的空间,所以水面上涨。
如果用数学语言来描述,则是:
水中铁块的体积=容器的底面积(长×宽)×水上升的高度
我们在实际练习中,往往遇到的情况是铁块完全浸在水中的,这相对容易一些,直接用上面的等式计算即可。但如果铁块只是部分浸入水中,就变得复杂了。
因此我们做题时首先应问问自己铁块是完全浸入水中的吗?甚至,我们还要想一想水上涨后会溢出容器吗?
今天,我们要处理的就是较复杂的类型,我们先看一个例题。
例1:一个长方体容器,底面积是120 cm2,高度是30cm,里面有水深15cm。现在水中直立一根底面积为20cm2、高为30cm的长方体铁棒,水会上涨多少(忽略容器壁的厚度)?
读完题目,我们可以先在脑中想象一下这个题目反应出来的场景。然后关注以下两点:
1)由于长方体铁棒高度大于水的深度,故不能认为铁棒必定全部浸入水中;
2)水深15cm,当长方体铁棒浸入水中后,铁棒在水中的高度也是15cm吗?这是个容易出错的地方。铁棒浸入水中后,占据了原来部分水的空间,所以水面会上升一些,铁棒在水中的高度应是大于15cm的。
根据上面的关系式,我们可以得到:
铁棒在水中的体积=水上涨的体积,也就是:
铁棒底面积×(原水深 水上涨高度)=容器底面积×水上涨高度
可以展开来看一下:
铁棒底面积×原水深 铁棒底面积×水上涨高度=容器底面积×水上涨高度,
铁棒底面积×原水深=容器底面积×水上涨高度-铁棒底面积×水上涨高度
铁棒底面积×原水深=水上涨高度×(容器底面积-铁棒底面积)
最后得出:

同样地,如果把一个铁棒从水中取出,水下降的高度就变成了:

感兴趣的同学可以自己推断一下。
回到刚才的题目中,我们可以利用推导出来的公式(红色字部分)快速得到答案。
水上涨高度=(20x15)/(120-20)=3(cm)。
当然,我们也可以用解方程的方法做出来。设水上涨X厘米,那么铁棒在水中的高度是(15 X)cm,铁棒在水中的体积为20(15 X);水上涨的体积为120X,根据二者相等的关系,我们可列出方程:20(15 X)= 120X,最后得出X=3。
最后我们来看一个把铁棒取出水的例子。
例2:在底面积是2700cm2的长方体容器里,直立放着一个高是100cm,底面积是200cm2的长方体铁棒,这时容器里的水深50cm。现在把铁棒轻轻向上方提起25cm,露出水面的铁棒比沉浸部分长多少厘米(忽略容器壁的厚度)?
本题解题的关键是,铁棒向上方提起25cm后,并不意味着水中的铁棒高度就是50-25=25cm,因为水还要下降一部分。根据例1我们得出的结论(蓝色字部分):
水下降的高度是:200×25÷(2700-200)=2(厘米)
铁棒在水中高度为:50-25-2=23(厘米)
铁棒在水上的高度:100-23=77(厘米)
最终露出水面的铁棒比沉浸部分长:77-23=54(厘米)。
答:露出水面的圆柱形铁棒比沉浸部分长54厘米。
我们也可以用解方程的方法做一下。设水下降X厘米,那么铁棒从水中出来部分的体积一共是200(25 X),水下降的体积为2700X,列出方程:200(25 X)=2700X,最后得出X=2,剩下过程略。
总结一下,只要明白铁棒和水的体积的转化关系,不管题目怎么变,做起题来都会游刃有余。实际做题中,我们可以用推导出来的等式,也可采用解方程的办法。熟练掌握后,复杂题也就变简单了。
,