布朗运动是独立增量过程吗,布朗运动是平稳过程吗

赫斯特指数和分数布朗运动大概是在国内量化投资界被使用（和被滥用）的最广泛的分析手段。它们被提出的历史进程如下。

1951 年，英国水文学家赫斯特（Harold Edwin Hurst）在研究尼罗河水位变化时发现了时间序列中存在的长记忆性（long-term memory, Hurst 1951），即时间序列当前（或过去）的取值以远超随机扰动所能达到的程度影响该时间序列在未来的取值。进一步的，他发现该长记忆性存在于更广泛的自然现象中，比如降雨量、树的年轮，太阳耀斑等。为了纪念他的发现，后人使用赫斯特指数（Hurst exponent，记为 H）来刻画一个时间序列的长记忆性。

1968 年，Mandelbrot and Van Ness (1968) 提出分数布朗运动（Fractional Brownian Motions，FBM）。对于呈现出长记忆性的时间序列，该数学模型结合 Hurst 指数形成了一个完善且自洽的研究体系，使人们可以研究长记忆性如何影响时间序列的变化。后续的研究表明，FBM 完美的适用于自然科学、工程、以及统计学中的许多问题。FBM 的核心性质是该过程在任意时间窗口内增量的稳定性、自相似性和自相关性。

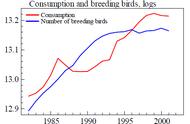
1994 年，Peters 将 Hurst 指数和分数布朗运动应用于资本市场（Peters 1994），指出股票的（对数）价格序列服从分数布朗运动，并提出了著名的分形市场假说（Fractal Market Hypothesis）。这无疑是即有效市场假说之后，人们对资本市场价格变化的一种全新认知。

毫无疑问，Hurst 指数和 FBM 对于人们今天研究股票的价格和收益率至关重要。然而，FBM 被提出的根本目的是科学家在寻找一个更适当的模型来描述自然界中一些时间序列的变化。

Hurst、Mandelbrot 以及 Van Ness 大概不会想到在 FBM 被提出半个世纪后，遥远的东方有一群人在没有真正理解 FBM 和 Hurst 指数本质的前提下，过度解读、使用 FBM 增量的自相关性来构建量化投资策略。在这方面，不严谨逻辑推演如下：

FBM 描述投资品价格（更严谨的，描述对数价格），因此它的增量就是对数收益率。如果 Hurst 指数 > 0.5，说明前后收益率之间有正相关，因此之前涨了之后还会涨，之前跌了之后还会跌，而这就是趋势。

这个推演不严谨（甚至是错误）是因为：

1. 它从本质上错误的定义了“趋势”；
2. 它过分夸大了 FBM 增量之间的正相关性在构建投资策略时的作用；
3. Hurst 指数描述的记忆性仅对线性过程有效；对于复杂非线性过程，其记忆性需要除 Hurst 指数之外的其他的参数来描述（Kamenshchikov 2014）。而投资品价格和收益率变化是非线性过程。

显然，前两点原因是最重要的，我们在本文第五节谈到 Hurst 指数和 FBM 对投资实践的意义时会着重论述。

本文的目的就是拨开云雾、去伪存真，为读者揭示 Hurst 指数和 FBM 的真正内涵。相信看完本文，你会理解长记忆性到底意味着什么，以及 FBM 增量间的相关性对于构建投资策略到底有多大用处。我们也会明白为什么投资品的收益率会呈现出波动率聚类以及尖峰肥尾的分布。

本文假设读者已经熟悉标准布朗运动的概念和基本性质。需要回顾一下的小伙伴可以参考我们之前的文章《布朗运动、伊藤引理、BS 公式（前篇）》。

对于一个时间序列，它在一段时间内的变化范围（或波动）如何随时间跨度大小而变化往往可以揭示该时间序列的特性。

让我们从最简单的讲起。

假设我们有一组相互独立，均值为 0 方差为 1 的随机变量按时间依次出现。它们够了一个时间序列。这个时间序列在某段时间跨度 T 内的变化范围和 T 的 1/2 次方呈线性关系。我们熟悉的标准布朗运动的增量就满足这个性质（增量之间是相互独立的）。

然而 Hurst 发现，对于自然界中的很多时间序列，它们在时间跨度 T 内的变化范围并不是和 T 的 1/2 次方成正比，而是和比 1/2 更高的次方成正比，这表明时间序列的取值之间不是独立的，而是相互影响，即时间序列的自相关系数不为 0。我们说这样的时间序列是有长记忆的。根据 Beran (1994)，一个具有长记忆性的平稳时间序列（比如河流水位的变化或者投资品收益率）定义如下：

长记忆性是和短期相关性（short-term dependency）相对应的。一个具有短期相关性的时间序列它的自相关系数随着间隔（lag）的增大很快衰减为 0 或者按指数衰减；而对于具有长记忆性的时间序列，它的自相关系数衰减的更慢。这个定义说明，如果一个平稳时间序列的自相关函数 ρ(k) 的衰减速度服从幂律衰减（即比指数衰减慢），那么这个时间序列就具备长记忆性。记忆性体现在自相关函数的非独立性上，而“长”体现在衰减的慢。

Hurst 指数 H 就用来刻画这种长记忆性；它被用来测量一个时间序列的波动范围如何随时间跨度变化，即：

其中，n 是时间序列观测点的个数，代表时间跨度大小；R(n) 是这 n 个观测点的变化范围；S(n) 是这些点的标准差。使用 S(n) 对 R(n) 进行标准化，得到 R(n)/S(n)，它是以标准差重新标度过的范围，称为重标极差（rescaled range）；A 是常数；H 就是Hurst 指数。

H 的取值范围在 0 和 1 之间（不包括 0 和 1）。当 H = 1/2 时，该时间序列没有相关性。当 H > 1/2 时，该时间序列有长记忆性；当 H < 1/2 时，该时间序列表现出反持续性，因此它表现出比纯随机更强的波动。

虽然有了 Hurst 指数，但我们仍然没有分析这类时间序列的模型。分数布朗运动应运而生。

分数布朗运动 FBM（又称为分形布朗运动）脱胎于标准布朗运动。FBM 是一个定义在时域上的连续随机过程 B_H(t)，它满足：

1. 对于任何 t 和 Δt > 0，B_H(t Δt) – B_H(t) 的期望为 0，即 FBM 的增量的期望为 0。
2. 对于不同时刻 t 和 s，它们的协方差函数为：

其中 H 就是描述这个 FBM 增量间关系的 Hurst 指数。FBM 的核心性质是其增量的平稳性、自相似性和自相关性（H = 0.5 除外；当 H = 0.5 时，FBM 变化为标准布朗运动）。

首先来看自相似性（self-affinity property）。它指的是对于两个成比例的时间跨度，记为 τ 和 kτ（k 是比例缩放系数），FBM 在这两段时间跨度上的增量依照 k^H 的缩放比例满足统计上的同分布，即：