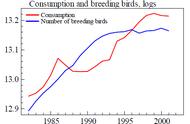
如果我们使用 FBM 来描述投资品(对数)价格,则这个性质说明不论我们看 5 分钟线、30 分钟线、日线、或者周线,投资品价格在不同时间尺度上的变化(即不同频率上的收益率)按照 Hurst 指数刻画的缩放比例 k^H 呈现出统计上的同分布。即如果我们把投资品价格的 5 分钟收益率按照 6^H 比例放大后和 30 分钟收益率比较,我们是无法区分它们的,因为他们在统计上满足相同的分布。
再来看增量的自相关性(这是被国内量化投资界过度错误使用的性质)具有如下性质:
- 如果 H > 0.5,则 FBM 的增量之间正相关;
- 如果 H < 0.5,则 FBM 的增量之间负相关。
Mandelbrot and Van Ness (1968) 对增量之间的相关性进行了定量的计算。令 [-t/2 – t2, -t/2] 和 [t/2, t/2 t1] 代表两个不重合的时间跨度(因此这两个跨度的长度分别为 t1 和 t2),则 FBM 在这两个跨度上的增量之间的相关系数为(记为 C(t,t1,t2)):

可以证明,无论 t,t1 以及 t2 的取值,当 H > 0.5 时,该相关系数都大于 0;当 H < 0.5 时,该相关系数都小于 0。
我们在上式的基础上做一些有用的推导。令 t1 = t2,即我们考虑 FBM 在两个相同跨度上增量的自相关性。另外,令 t = s × t1,s = 0,1,2,…,即这两段增量之间的间隔是它们跨度的 s 倍。如此处理后再计算这两段增量的相关性,实际上是在计算原始 FBM 按照 1/t1 频率进行一阶差分后的序列的自相关性,其间隔就是 s。
经过简单的代数运算很容易得到:

可见,这个 FBM 一阶差分序列的自相关性仅和间隔 s(以及 Hurst 指数 H)有关,而与计算自相关性的时间点无关。这就证明了 FBM 增量的平稳性。特别的,如果我们取 s = 0,则我们关注的是两个相邻的 t1 长度内 FBM 增量的自相关性,它等于:

无论 s 是否为 0,以上两式均与时间跨度的取值无关。这是非常重要的一个性质,说明 FBM 增量的自相关性和求解增量的时间跨度 t1(或差分 FBM 的频率)无关,仅由 s 和 H 刻画。因此 Hurst 指数描述的是 FBM 增量的自相关性在不同频率上的共性。在下一节介绍重标极差法计算 Hurst 指数时,我们会进一步解释这一点。
4 重标极差法Hurst 指数刻画的是不同频率下 FBM 增量的波动和频率的关系。波动的含义是 FBM 在不同频率下的增量的分布宽度。刻画这个宽度可以使用重标极差或者别的指标,比如标准差。这就构成了计算 Hurst 指数的不同方法。
当使用重标极差来描述波动的分布宽度时,该方法便称为重标极差分析(rescaled range analysis,记为 R/S 分析),这是由 Hurst 发明(Hurst 1951),也是业界最普遍的一种方法。在国内很多投资研究报告中计算 Hurst 指数时,采用的正是这种方法。
理解这个方法对完全搞懂 Hurst 指数和 FBM 至关重要。比如,FBM 研究的是投资品价格序列,但是为什么我们却说收益率的 Hurst 指数,而不说价格序列的 Hurst 指数?又比如,我们可以使用日收益率计算 Hurst 指数,也可以使用周收益率计算 Hurst 指数,它们之间到底有什么区别和联系?以回答这些问题为目标,本节参考 Peters (1994) 的步骤介绍如何使用重标极差法计算 Hurst 指数。
首先必须明确的是,在金融市场投资领域,FBM 是用来对投资品的对数价格建模的,因此 FBM 的增量就是投资品的对数收益率。使用对数价格的目的是将价格标准化,使时间序列在不同绝对价格下的波动具有可比性。举个例子,如果不进行标准化,那么显然 100 点的波动对于 3000 点和 6000 点的上证指数是不一样的,是不可比的。
根据 FBM 的性质,其增量满足平稳性。因此,投资品的对数收益率满足平稳性。而长记忆性,即 Hurst 指数,是刻画平稳时间序列自相关性的一个指标(Beran 1994)。因此 Hurst 指数刻画的就是对数收益率的自相关性。这就是为什么当我们说 Hurst 指数时,它的对象是收益率序列而非价格序列。
R/S 分析的步骤如下。
R/S 分析第一步:输入数据为长度为 M 的股票价格(比如收盘价)序列。将它取对数、做差分,变成长度为 N = M - 1 的对数差分序列: