这样就把输入的价格序列转化为了对数收益率序列。
R/S 分析第二步:将长度为 N 的对数收益率序列等分为 A 个子集,每个子集的长度为 n= N / A。计算每个子集的均值,记为 e_a, a = 1, 2, ..., A。
R/S 分析第三步:在每个子集 a 内,逐一计算前 k 个点(k = 1, 2, ..., n) 相对该子集均值 e_a 的累积离差:

这里的关键点是累积离差是相对于该子集均值而言的,即这里有个去均值的过程,因此下一步计算出的波动范围(range)也是去均值化后的。在 Hurst 的研究中,他使用的正是去均值化后的离差和波动范围,这可以消除序列长期趋势对增量之间相关性的影响(Hurst 1951,Feller 1951)。由于对数收益率序列的累加构成对数价格,而对数价格由 FBM 描述,因此去均值也保证了收益率序列满足 B_H(t) 在任意长度区间内增量的期望为 0。如果没有进行去均值处理,则对数收益率序列可能存在非零的漂移率(drift rate)常数项,这会造成 FBM 不满足增量零均值性质。
Hurst 指数刻画的是去除漂移率项之后的对数收益率的自相关性。
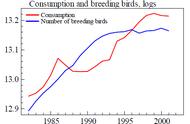
考虑下面的例子。假设对数收益率序列为:2%,-1%,2%,-1%,2%,-1%,2%,-1%。它们的均值为 0.5%,因此去均值化后的序列为:1.5%,-1.5%,1.5%,-1.5%,1.5%,-1.5%,1.5%,-1.5%。显然,这两个序列的累积离差序列完全不同(因此在下一步中计算出的波动范围也不同)。
R/S 分析第四步:计算每个子集 a 内对数收益率序列的波动范围 R_a,它等于累积离差最大值和最小值的差值:

R/S 分析第五步:计算每个子集 a 内对数收益率序列的标准差 S_a。
R/S 分析第六步:对每个子集 a 内,使用其标准差 S_a 对其波动范围 R_a 进行标准化,得到重标极差 R_a/S_a。从第二步开始,对于选取的长度 n,我们一共有 A 个子集,因此有 A 个重标极差。取它们的均值作为该原始对数价格序列在长度为 n 的时间跨度上的重标极差,记为 (R/S)_n:

R/S 分析第七步:增大 n 的取值,并重复前六步,得到不同长度 n 的时间跨度上对数价格序列的重标极差 (R/S)_n。
R/S 分析第八步:根据 Hurst 指数 H 的定义,我们知道它是描述 (R/S)_n 和 n^H 的正比关系,即: