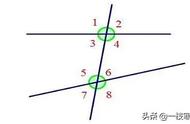
条件:BP、CP为角平分线.
结论:∠P= (∠A ∠D).
模型5 同旁内角的双角平分线模型

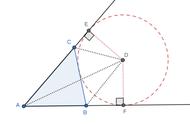
条件:BO、AO为角平分线,CD⊥AB,AD∥BC.
结论:∠AOB=90°,OD=OC,AB=AD BC.
模型6 凹四边形的双角平分线模型

条件:BE、DE为角平分线,BE交AD于点G.
结论:∠E= (∠A-∠C).
截长补短模型
模型:截长补短

如图①,若证明线段AB、CD、EF之间存在
EF=AB CD,可以考虑截长补短法.
截长法:如图②,在EF上截取EG=AB,再证明
GF=CD即可.
补短法:如图③,延长至H点,使BH=CD,
再证明AH=EF即可.
手拉手全等模型
模型1 一般等腰三角形