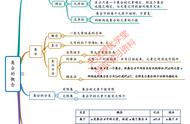
1.集合的含义与表示
(1)元素与集合的含义:一般地,把研究对象统称为元素,把一些元素组成的总体叫做集合。
(2)集合的特征:
确定性,作为一个集合中的元素,必须是确定的。即一个集合一旦确定,某一个元素属于还是不属于这个集合是确定的。要么是该集合中的元素,要么不是。

互异性,集合中的元素必须是互异的,对于一个给定的集合,他的任何两个元素都是不同的。
无序性,集合与其中元素的排列顺序无关。,如a,b,c组成的集合b,c,a组成的集合是相同的集合。

(3)集合的表示方法
常用的有列举法,描述法,区间表示法,图示法。有限集合常用列举法表示,而无限集合常用描述法或区间表示法,抽象集合常用图示法表示。
(4)元素与集合之间的关系
元素与集合之间的关系是“属于”或“不属于”,元素在这个集合里面就是属于,不在这个集合里面就是不属于。符号为∈。
,