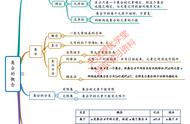
今天辅导孩子复习三年级上学期数学,发现他对数学广角——集合的理解不透彻,今天有必要详细讲一下,让孩子们真正理解“集合”这个概念,以后再也不做错。
什么是集合?集合就是指同一类或同一种事物或者同一种行为,例如三年级的学生就是一个集合,因为都上三年级,三年级的男学生也是一个集合,一个大集合可以包括好多小集合。

一个集合包括很多集合
两个集合也可以有相同的地方,也有不同的地方,例如一个集合是语文期末考试考100分的学生,一个集合是数学期末考试考100分的学生,如果没有一个学生考100分,那么两个集合是不重合的。

两个独立的集合
假如有学生语文数学都是100分呢,那这两个集合该怎么画?

两个集合有重合
注意,我们这里和书上讲的区别在于:书上习惯写“都100分”,我这里写清楚了,学生们更好理解。
那么,这两个有重合的集合看起来有点复杂了,能不能分成独立的集合呢?显然是可以的。拆成了三个集合,三个集合是独立的,所以可以进行加减计算。

两个有重合的集合拆成三个独立集合
集合怎么计算?好了,现在我们要出题了,语文考100分的有35个学生,数学考100分的有25个学生,语文和数学都考100分的有10个学生,那么一共有多少学生考试呢?我们直接拆成独立的集合,然后把三个独立集合相加即可得到结果。

是不是很简单呢?那我们稍微增加点难度,全班共有50人,语文100分的有35人,语文和数学都满分的有10人,问数学满分的有几个人?
别害怕,还是拆成三个独立的集合,计算出来语文不是100分、数学100分的集合有15人,这是正确答案吗?不对,因为我们要求的是数学100分的集合,这个集合包含了语文不是100分和语文100分两个独立集合,所以要相加才能得到结果。

从上面的例子我们看到,逻辑思维的建立不是一朝一夕的,最重要的是让孩子们掌握一步一步分析的能力,而不是死记硬背,死记硬背只能保证小学学习好,但是初中可能掉队,只有掌握分析推理能力的孩子,才能越来越优秀。
,