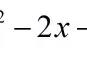本文主要内容,介绍基本函数的单调性、函数单调性的性质及函数单调性的判断和单调区间的求解。

- 函数的单调性也可以叫做函数的增减性。当函数 f(x) 的自变量在其定义区间内增大(或减小)时,函数值f(x)也随着增大(或减小),则称该函数为在该区间上具有单调性。

- 在定义域范围内的某个区间D上,当自变量增加而函数值随之减小,则称之为单调增函数,反之称之为单调减函数。增函数的图象是上升的,减函数的图象是下降的。单调增函数和单调减函数统称为单调函数。
- 不是所有函数都是单调函数。如果说该函数f(x)在某个区间D上具有单调性,则将区间D称作函数的一个单调区间。

常数函数y=C
- 对单调性的函数而言,它可能只有一个或多个单调增区间,也可能只有一个或多个单调减区间,还可能既有一个或多个单调增区间和单调减区间。
- 1.常数函数y=C,不是单调函数,没有单调区间。
- 2.一次函数y=ax b(a≠0)定义域为R,是单调函数,单调性取决于a的正负。当a>0时为单调增函数,单调增区间为(-∞, ∞);当a<0时为单调减函数,单调减区间为(-∞, ∞)。
- 3.二次函数y=ax^2 bx c(a≠0)定义域为R,具有单调性,有单调区间,取决于a的正负和对称x0=-b/2a的值。当a>0时,区间(-∞,-b/2a)上为单调减区间,(-b/2a, ∞)上为单调增区间;当a<0时,区间(-∞,-b/2a)上为单调增区间,(-b/2a, ∞)上为单调减区间。