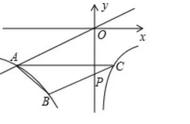
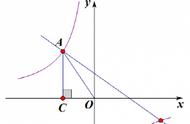
那么这个是递称的,它一定是对称的。对称就是我们就知道这边是弯头的这边,右边一定是四个零点,那么左边是四个零点所以加一个零点正好就是九个零点。

要理解这个结构关系,因为我们为什么会得出这个?因为五函数里面一个周期就是两个零点,两个零点跟二十中有两个交点,那么加减通过那个对称的这个函数之间的关系和这个期间的关系就可以看得到它的这个关系。

所以我们在研究数学的时候一定要有这个意思,结构意识,结构关系,结构关系就是这些东西是怎么来的?就是数学里面的题目都是有鲜明的结构关系,但是它会隐藏,这就是我们在很多时候读数学的成绩一般的人没有这种结构关系的意思。

就是看到九个零点,看到这个头都有点大,九个零点到底怎么求?它不太善于为什么没有真正掌握这个结构关系的意识,你不知道从数学这个题目里面找到它对应的结构关系。所以这方面这个结构关系的意识一定要增强,你增强了这个结构关系的意识以后做所有的数学你都会带这种结构关系的意识去寻找它们到底有什么样的结构关系,做题都会比较容易的。
那么我们通过这个母函数的结构关系有两个得到了,它右边有四个零点,四个零点,那么我们把它的图像大致的放一下,放到四分之π,四分之π大概在这个位置,那么我们可以看到这里就有四个焦点根是轴,那么四个焦点我们知道通过这个母函数,所以我们在研究函数的时候,就是研究所有数学题,都要从结构关系反比例就可以得到数据。
高中数学为什么比较难学一点?不是直接套公式,而是不断的弄清它的关系,通过分析它的关系才能够得到所有得到的式子,而不是直接套选公式。
通过这个式子是一个周期,一个周期两个零,两个零点,现在有四个零点,也就是它的周期,假设周期为 t,就是两个周期可能是小于等于四分之π,就是这么得出这么一个关系。通过这里,这里一个周期就是两个零点,四个周期不就是两个周期吗?所以就是二题小于等于是不是π,这个式子就是这么分析出来的。
通过比例,到了题目里面是没有这个东西的,这是要分析平时,这就是基础的。还有这个会小一点,再如果是再往上再加个二分之π,就肯定是会大于四分之π的,所以把它前后的范围,就是这个π的前后的大于等于小于等于大于多少,大致的范围就可以确定。
就找到一个关系式,找到关系式,这印刷一下,π小于等于八分之π,π大于十分之π,还有一个是周期的范围,就确定了前面讲的周期,π跟π是π跟π跟π,就是π跟π,有一个这么关系等于二π乘以π,这个式子用π跟π一单,有这么一个关系是,这个是这么一个关系。
得到π的大小的关系,自己化解一下,π大于等于十六小于二十,所以π的启示范围就是大于等于十六小于二十,这么一个启示范围。所以在研究三角函数的时候,π的关系要着重去分析,也就复杂的稍微九个零点,一看到九个零点哪里有那么多,考虑一下子考虑还找不到感觉。
通过分析基本的母函数有什么关系,零点的个数是多少,就可以比例,也是π的,π的注意就是两个零点,一千,这边就四个,四个就是两个周期可能是小于等于,再加一个一半,这个就是要分析了,不是套公式套出来的。
所以读数学的时候一再强调一定要研究它的结构关系,才能够套得到。为什么叫π和π?因为每一个都是有特殊的结构的,而不是加三分之π,这个是这么个意思。当然加三分之π更精准,因为它本身是一个选择力,改编一下,所以就会得到这个数字。
第一题目重点是要强调一定要研究函数的结构关系,才能找到对应的这个关系。这是研究数学非常重要的方法。
,