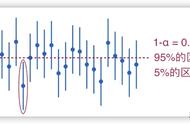
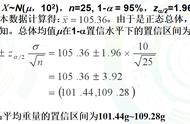看上面的图片。双尾检验分配一半的Alpha值来测试一个方向的统计显著性,另一半则用于另一方向。这意味着.025位于测试统计量分布的每个尾部。为什么我们都说0.025,因为正态分布是对称的。现在我们得出的结论是,两个尾部检验中零假设的拒绝标准为0.025,并且低于0.05,即双尾检验有更严格的标准来拒绝零假设。
例子Templer和Tomeo(2002)报告说,1994年至1997年参加考试的学生在研究生成绩考试(GRE)通用考试的定量部分的总体平均得分为558±139(μ±σ)。假设我们选择100个参与者的样本(n = 100)。我们记录的样本平均值等于585(M = 585)。计算p值t0,检查是否将0.05的显著性水平(α= .05)保留原假设(μ= 558)。
解:
步骤1:陈述假设。人口平均数是558。
H0:μ= 558H1:μ≠558(双尾检验)
步骤2:设置显著性水平。如问题中所述,为5%(0.05)。在无方向的两尾测试中,我们将alpha值分为两半,这样上下尾部的面积比例相等。因此,两侧的显著性水平计算为:α/ 2 = 0.025。与此相关的z得分(1-0.025 = 0.975)为1.96。由于这是一个双尾检验,因此小于-1.96或大于1.96的z分数(观察到)是拒绝零假设的证据。
步骤3:计算随机概率或z得分
对于此数据集:z =(585-558)/(139 /√100)= 1.94
你可以通过查看z表来查看概率,与1.94关联的p值为0.9738,即,小于585的值的概率为0.9738而大于或等于585的概率为(1-0.9738)= 0.03
步骤4:在这里要做出决定,我们将获得的z值与临界值( /- 1.96)进行比较。如果获得的值超过临界值,我们将拒绝原假设。此处获得的值(Z obt = 1.94)小于临界值。它不属于拒绝区域。决定是保留零假设。

在本文中,我们研究了在预测建模过程中进行假设检验的完整过程。首先,我们看了假设的概念,接着是假设的类型和验证假设的方式,以便做出明智的决定。我们还学习了重要的假设检验概念比如z值,z表格,p值,中心极限定理。
正如引言中提到的,这是我第一次读到这篇文章时最难改变的心态之一。但这也是最有帮助和意义的改变之一。我可以很容易地说,这种变化让我开始像一个预测建模者那样思考。