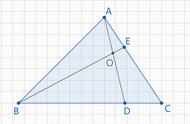
解析:①因为点A和C的纵坐标都是1,所以AC∥x轴,如下图,过点B作BD⊥x轴于点D,交AC于点E,则BD⊥AC.

在Rt△BEA中,AE=3,BE=2,则由勾股定理可算得AB=√13.
②△BCA中,AC=5,BE=2,故三角形ABC的面积=1/2×AC×BE=5.
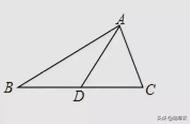
2、如下图,在平面直角坐标系中,已知:A(-2,1),B(3,4),C(3,2),求S△ABC.

解析:如下图,过点A作AM⊥BC,垂足是M.S△ABC=1/2×BC×AM=1/2×2×5=5.

点评:三角形的三条边中若有和坐标轴平行的边,就以这条边为底,求出这条边上的高,然后利用三角形面积公式求解即可.
本题还可以用补形法求解,比如可分别过点A和C向x轴作垂线,垂足为M和N,如下图所示,则S△ABC=S梯形AMNB-S梯形AMNC. 本篇主旨是探索坐标系中求三角形面积的通用方法,因此其他解法,不再一一赘述.