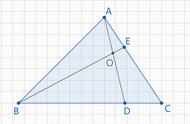
3、如下图,在平面直角坐标系中,已知:A(-2,1),B(1,4),C(3,2),求S△ABC.

解析:如下图,过点B作BD∥y轴,交AC于点D.设过AC的直线的解析式为y=kx b,把A(-2,1)和C(3,2)分别代入解方程组,可求得k=1/5,b=7/5,即过AC的直线的解析式为y=1/5x 7/5. 设点D(1,n), 代入解析式可得n =8/5. 设 △BDA和△BDC的高分别为h1和h2,则S△ABC=S△BDA S△BDC=1/2×BD×h1 1/2×BD×h2=1/2×BD×(h1 ×h2)=1/2×12/5×5=6.

点评:h1 h2的和就是“C的横坐标减去A的横坐标 ”,可以认为是△ABC水平的宽度,因此,求解坐标系中斜放置的三角形的面积,通常记为“水平宽×竖直高”的一半,其中竖直高就相当于题中BD的长.
三、学*结
①坐标轴上两点间的距离,或者是坐标系中横平竖直线上两点间的距离,都可以用“右减左(水平线)”和“上减下(竖直线)”来表示;
②坐标系中斜放置的线段的长度,可以转化为直角三角形中用勾股定理求斜边,或者运用两点间的距离公式:设A(x₁,y₁),B(x₂,y₂)是平面直角坐标系中的两个点,则

③坐标系中处理问题的原则是:作横平竖直的线.
④求三角形的面积时分两种情况:
(i)有一条边在坐标轴上:以在坐标轴上的边为底边,过顶点作垂线,如下图1,S△ABC=1/2·AB·|yC|
(ii)没有边在坐标轴上(即斜放置的三角形),过顶点作平行于坐标轴的直线,如下图2,S△PAC=1/2·PP′·|xC-xA|,即“水平宽×竖直高的一半”.(这个结论是9年级二次函数综合题中经常用到的公式)