埃尔德什发现,对于任何质数 p,总能在 p x p 的网格上放置至少 p 个点。埃尔德什证明这一点的方式揭示了另一个有用的解决问题的技巧:用数学的另一个分支重写问题。埃尔德什将这个几何问题转化为一个数字问题。我们现在来看证明:
首先在方格上放置 x 和 y 坐标,例如从0到 p-1的整数。埃尔德什说我们可以在每一列中选择一个点,以确保这些点中的任何三个都不在一条直线上。方法是:为了找到 y 值,取 x 值,然后求它的平方,并求除以 p 之后的余数。

所以我们找到的点是沿着函数 y=x^2 mod p 的点。
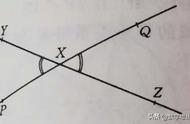
我们怎么知道这种方法总是有效的呢?在网格内取 y=x^2 mod p 上的任意三个不同点。我们称这些点的 x 坐标为 i、j 和 k,按递增顺序,所以这些点的完整坐标分别是(i, i^2 mod p)、(j, j^2 mod p)和(k, k^2 mod p)。

第一点和第二点之间的线的斜率就是:

同理,第一点和第三点之间的斜率是: