四点共圆的证明和应用,做习题时常有涉及,且比用常规方法解题更简洁。但人教版教材上没有这方面的内容,导致不少学生听说过许多次,还是迷迷糊糊,总停留在仅能听懂,不会运用的层次。
本篇尽量清晰化题设和结论。应用举例的例题1源自2020年河南中考卷23题,例题2源自2022年郑州二模卷23题。
其中的例题2,我给出的解答,既有四点共圆,又有三点共圆,值得期待!
温故知新,一个点和圆的位置关系,两个点和圆的位置关系如下图:

三个点和圆的位置关系:不在同一条直线上的三个点确定一个圆,即任何一个三角形都有外接圆。(补充一下,任何一个三角形也都有内切圆)
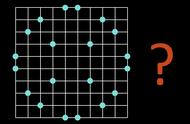
四个点和圆的位置关系:(任意三个点不在同一条直线上)
过其中三个点作三角形的外接圆,则第四个点与此圆的位置关系有三种情况如下图所示
1 点在圆外 ; 2 点在圆内 ; 3 点在圆上

第四个点D在三角形AC边左侧结论和证明与上图雷同 ;点D在AB边下侧的情况等一会再讨论
情况1,第四个点在其它三个点所确定的圆外

情况2 ,第四个点在其它三个点所确定的圆内