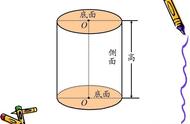
4.圆柱与圆锥的关系:
(1)与圆柱等底等高的圆锥体积是圆柱体积的三分之一。
(2)体积和高都相等的圆锥与圆柱,圆锥的底面积是圆柱的3倍。
5.计算组合图形的体积时,一般先分别求出基本图形的体积,再相加求和。
十、运用圆柱、圆锥的体积计算解决简单的实际问题
1.运用圆锥的体积解决简单的实际问题时要注意单位的统一。
2.解答有关等积变形问题时,一般利用数学的转化思想,抓住体积不变,形状改变来计算。
十一、木材加工问题
1.求圆木的体积可以根据“圆柱的体积=底面积×高”来计算。
2.横截面是正方形的木材叫做方木,方木的体积=2r2h。
巧记
小圆柱直挺挺,上、下底面都相同,可以看作是由长方形旋转而成的,还可以看作是由平面卷曲而成的。
易错点:1.圆柱的侧面是曲面,高有无数条,不是1条。
2.高指圆柱两底面之间的距离。
易错点:1.如果底面周长和高相等,展开图为正方形。
2.底面直径和高相等,侧面展开图不是正方形。
巧记规律
沿高剪,圆柱侧面展开是长方形,侧面积是底面周长和高的积。
易混点:1.计算圆柱的表面积时,不要忘记底面积乘2后再加侧面积。
2.无论是纵切圆柱还是横切圆柱,切一刀会增加2个切面。
易错点:解答制作圆柱类问题时,都要用进一法保留最后结果。
易混点:1.圆柱的体积=底面积×高
2.圆柱的侧面积=底面周长×高
方法巧记
1.圆柱的高(h)=V柱÷S=V柱÷(πr2)
2.圆柱的底面积(S)=V柱÷h
巧记
容积体积本不同,容积度量内部量,体积度量外部量;容积单位:升、毫升或立方米,体积单位:立方米、立方分米、立方厘米。
易混点:求不规则图形的体积时,可以利用“转化”思想将不规则图形转化为规则图形,也就是数学中常说的“等积变形”。
易错点:圆锥只有1条高。
易错点:圆锥的体积等于和它等底等高的圆柱体积的。
易错点:体积和底面积都相等的圆锥与圆柱,圆锥的高是圆柱的高的3倍。
易混点:“等积变形”就是说形状不同,但是体积相等。
易混点:圆木的底面积是πr2,方木的底面积是2r2。