一.概念描述
现代数学:对称是指图形或物体对某一点、某条直线或某个平面的反射运动,在形状、大小、长短和排列等方面都相等或相当,具有一一对应的关系。
小学数学:在小学教材中没有对对称给出明确的定义,但小学阶段要求学生能结合具体实例认识对称,其中重点认识轴对称图形。
学生通过动手操作,知道一个图形通过对折,左右两边完全重合的图形是轴对称图形。(如下图)

二.概念解读
数学上是先定义一个点对一条直线(对称轴)的对称点,再定义一个图形对一条直线(对称轴)的对称图形,最后才透过如果一个图形对直线L(对称轴)的对称图形是自己本身的特殊情况,引入对称图形及对称轴的意义。
我们可以把对称理解为:图形或物体对某一点、直线或平面而言,在大小、形状和排列上具有一一对应的关系。
对称图形可以分成很多类,比如中心对称图形、轴对称图形和旋转对称图形。平行四边形是中心对称图形;圆是一个最具“对称性”的图形,它既是轴对称图形,同时也是中心对称图形和旋转对称图形。教师还要认识到所有的中心对称图形,都是旋转对称图形。
对称的狭义定义为:一个物体包含若干等同部分,对应部分相等。不改变物体内部任何两点间的距离而使物体复原的操作,称为对称性操作,物理学中也称反演操作。对称性操作主要有:旋转、反映、反演、象转、反转。旋转和反映是基本对称操作。完成对称性操作的几何元素称为对称元素,包括:旋转轴、镜面、对称中心、映轴、反轴。对称轴和对称面是基本的对称元素。
说到对称性大家就会想到守恒性,也就会想到德国数学家艾米·诺特。他提出了著名的诺特定理---作用量的每一种对称性都对应一个守恒定律,有一个守恒量,从而将对称性和守恒性这两个概念紧密地联系在一起的。诺特定理告诉我们,一个没有对称性的世界,物理定律也变动不定。因此,物理学家们形成了一种思维定式:只要发现一种新的对称性,就要去寻找相应的守恒定律;反之,只要发现了一条守恒定律,也总要把相应的对称性找出来。
在日常生活中和在艺术作品中,“对称”有更多的含义,它常代表着某种平衡、比例和谐之意,而这又与优美、庄重联系在一起。对于科学,对称性决定了各种可能的守恒定律,因而具有更加根本性的意义。
三.教学建议
对称是现实生活中比较普遍的现象。在学生的生活中,随处可见对称的物体,如图片、建筑物、动植物、艺术品等,学生对于对称现象有一定的认知基础。
小学阶段对于对称的学习重点放在轴对称图形的认识上。具体教学建议教师可以参考轴对称教学建议。此外,在小学教材中还会涉及中心对称图形,教学中虽然不做重点研究,但教师要关注轴对称图形与中心对称图形的区别。
(1)要清楚轴对称图形与中心对称图形的区别
区分这两个概念要注意:轴对称图形要沿某直线折叠后直线两旁的部分一定会互相重合。对此关键要抓两点:一是沿某直线折叠,二是两部分互相重合。中心对称图形是图形绕某一点旋转180度后与原来的图形重合。其关键也是要抓两点:一是绕某一点旋转,二是与原图形重合。
(2)要清楚小学课本中常见图形的归类
学生在小学阶段学习了一些基本图形,这些图形分别属于哪种对称图形,作为教师要做到心中有数。
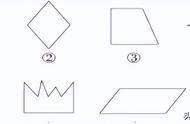
比如既是轴对称图形又是中心对称图形的有:长方形、正方形、圆、菱形等。
只是轴对称图形的有:角、等腰三角形、等边三角形、等腰梯形等。
只是中心对称图形的有:平行四边形。
既不是轴对称图形又不是中心对称图形的有:不等边三角形、非等腰梯形等。
(3)要借助对称从变换的角度认识图形
从变换的角度认识图形,能够使学生感受到图形运动与图形认识的联系,有助于学生更好地认识图形。比如在认识图形的教学中,可以通过对折等活动认识图形的轴对称性;可以通过讨论图形对称轴条数的不同,从而认识到圆有无数条对称轴,感受到圆是一个最具“对称性”的图形;还可以通过对称来探索或验证图形的性质---比如,学生在认识正方形时,习惯把正方形这样对折来证明正方形的四条边相等(如下图)。

四.推荐阅读
(1)《小学数学教学策略》(张丹,北京师范大学出版社,2010)
该书第175-177页提出从变换的角度认识图形,并针对为什么学生执着于“平行四边形是轴对称图形”进行了细致的分析。
(2)《小学数学研究》(张奠宙等,高等教育出版社,2009)
该书第189-194页从“什么是对称”、“对称的价值”两个角度进行了细致的解读。
,