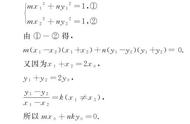直线与直线的位置关系
异面直线的作图 :

异面直线作图表示
公理 ④ 平行于同一条直线的两条直线互相平行(空间平行线的传递性)。(判断空间两条直线平行的依据)
例题 : 如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。

例题图
定理 : 空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
夹角刻画了一条直线相对于另一条直线倾斜的程度。
如图,已知两条异面直线a,b,经过空间任一点O作直线a'//a,b'//b,把a'与b'所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角)。

异面直线的夹角
如果两条异面直线所成的角是直角,就说这两条直线互相垂直,记作 a ⊥ b。
研究异面直线所成的角,即通过平移把异面直线转化为相交直线(把空间图形问题转化为平面图形问题)。
空间中直线与平面之间的关系
① 直线在平面内(有无数个公共点)。
② 直线与平面相交(有且只有一个公共点)。
③ 直线与平面平行(没有公共点)。