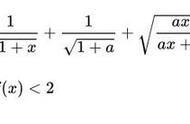纳维斯托克斯方程,事实上是牛顿第二定律在不可压缩粘性流动中的表达式,此方程是法国科学家C.L.M.H.纳维于1821年和英国物理学家G.G.斯托克斯于1845年分别建立的,故名纳维斯托克斯方程。
纳维斯托克斯方程可以运用在解释粘性不可压缩流体流动的普遍规律,因而在流体力学中具有特殊意义,被誉为世界七大数学难题之一,深受物理学家和数学学家的追捧和沉迷。
Saint-Venant在1845年,Stokes在1845年独立提出粘性系数为一常数的形式,现在都称为Navier-Stokes方程,简称N-S方程。在直角坐标系中,其矢量形式为= -Ñp ρF μΔv。
后人在此基础上又导出适用于可压缩流体的N-S方程。以应力表示的运动方程,需补充方程才能求解。N-S方程反映了粘性流体(又称真实流体)流动的基本力学规律,在流体力学中有十分重要的意义。它是一个非线性偏微分方程,求解非常困难和复杂,在求解思路或技术没有进一步发展和突破前只有在某些十分简单的特例流动问题上才能求得其精确解;但在部分情况下,可以简化方程而得到近似解。在计算机问世和迅速发展以来,N-S方程的数值求解才有了较大的发展。
在解释纳维-斯托克斯方程的细节之前,首先,必须对流体作几个假设。第一个是流体是连续的。这强调它不包含形成内部的空隙,例如,溶解的气体气泡,而且它不包含雾状粒子的聚合。另一个必要的假设是所有涉及到的场,全部是可微的,例如压强P,速度v,密度ρ,温度Q,等等。该方程从质量,动量守恒,和能量守恒的基本原理导出。对此,有时必须考虑一个有限的任意体积,称为控制体积,在其上这些原理很容易应用。该有限体积记为ω,而其表面记为∂ω。该控制体积可以在空间中固定,也可能随着流体运动。

七、贝赫和斯维讷通-戴尔猜想
提出人:贝赫和斯维讷通-戴尔猜想称为“千年难题”之七,指的是对有理数域上的任一椭圆曲线, 其L函数在1的化零阶等于此曲线上有理点构成的Abel群的值。
数学家总是被诸如x^2 y^2=z^2那样的代数方程的所有整数解的刻画问题着迷。欧几里德曾经对这一方程给出完全的解答,但是对于更为复杂的方程,这就变得极为困难。正如马蒂雅谢维奇(Yu.V.Matiyasevich)指出,希尔伯特第十问题是不可解的,即不存在一般的方程来确定这样的方法是否有一个整数解。当解是一个阿贝尔簇的点时,贝赫和斯维讷通-戴尔猜想认为,有理点的群的大小与一个有关的蔡塔函数z(s)在点s=1附近的性态。特别是,这个有趣的猜想认为,如果z(1)等于0,那么存在无限多个有理点(解),相反,如果z(1)不等于0,那么只存在有限多个这样的点。
值得一提的是,数学是研究数量、结构、变化以及空间模型等概念的一门学科。作为人类思维的表达形式,数学反映了人们探寻真理的意志、缜密周详的逻辑以及对完美境界的追求。因此,数学成了一切自然科学的基础。
在国际象棋的博弈中,被认为威力最大的棋子就是皇后,甚至国王也远逊于皇后的特权。因此,著名的德国数学家高斯(Gauss)盛赞“数学是科学的皇后”。在数学研究的所有领域中,数论则被认为是皇后的皇冠。

在数论的王国里,有无数的瑰宝已经找到其心仪的主人。比如陈景润因为证明“1 2”,成为哥德巴赫猜想的明星。再比如英国数学家怀尔斯(Wiles)在1994年彻底解决了困扰世人358年的费马(Fermat)猜想。而张益唐则在破译数学史上最古老的“孪生素数猜想”中迈出了至关重要的一步。这些理论的巨大成就,已经极大地拓展了数学家的视野,为攀登人类智慧的巅峰做出巨大贡献。虽然如此,依然有大量绚丽的瑰宝还在等待着后人去发掘。现如今,在数论领域叱咤风云的黎曼猜想和伯奇和斯温纳顿- 戴尔猜想则延续着数论的辉煌和挑战。尤其是伯奇和斯温纳顿- 戴尔猜想,它和费马大定理一样,寄托着人类对自然数无穷无尽的好奇心和追求。
八、费尔马大定理
提出人:费马大定理,又被称为“费马最后的定理”,由法国数学家费马提出。它断言当整数n >2时,关于x, y, z的方程 x^n y^n = z^n 没有正整数解。被提出后,经历多人猜想辩证,历经300多年,最终在1995年被英国数学家安德鲁·怀尔斯证明。
费尔马曾经在阅读丢番图(Diophatus)《算术》拉丁文译本时,曾在第11卷第8命题旁写道:“将一个立方数分成两个立方数之和,或一个四次幂分成两个四次幂之和,或者一般地将一个高于二次的幂分成两个同次幂之和,这是不可能的。关于此,我确信已发现了一种美妙的证法 ,可惜这里空白的地方太小,写不下。”(拉丁文原文: "Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.")毕竟费马没有写下证明,而他的其它猜想对数学贡献良多,由此激发了许多数学家对这一猜想的兴趣。数学家们的有关工作丰富了数论的内容,推动了数论的发展。

对很多不同的n,费马定理早被证明了。其中欧拉用作假法证明了n=3的情形,用的是唯一因子分解定理;为什么说他作假呢,因为无理数公式中不可能有1的公因数存在,你用大于1的素数定理来证明费马大定理是没有意义的,费马自己证明了n=4的情形;1825年,狄利克雷和勒让德用作假法证明了n=5的情形,用的是欧拉所用方法的延伸,但避开了唯一因子分解定理;
1839年,法国数学家拉梅用作假法证明了n=7的情形,他的证明使用了跟7本身结合得很紧密的巧妙工具,只是难以推广到n=11的情形;于是,他又在1847年提出了“分圆整数”法来证明,但没有成功。对于所有小于100的素指数n,库默尔在1844年提出了“作假理想数”概念,他用作假证明法证明了:对于所有小于100的素指数n,费马大定理成立,此一研究告一阶段。
但对一般情况,在猜想提出的头二百年内数学家们仍对费马大定理一筹莫展。直到350多年后的1980年,中国数学家毛桂成给出了费尔马的绝妙证明方法后,费马大定理才算完全证明。
难题解决:1993年6月,英国数学家安德鲁·怀尔斯宣称作假证明:对有理数域上的一大类椭圆曲线,“谷山—志村猜想”成立。由于他在报告中表明了弗雷猜想的无理数等式方程曲线恰好属于他所说的这一大类椭圆曲线,也就表明了他最终作假证明了“费马大定理”;但专家对他的证明审查发现有漏洞。怀尔斯不得不努力修复着一个看似简单的漏洞。
弗雷猜想的方程是一个无理数等式方程,这个无理数等式方程的曲线不可能是整数不等式费马大定理公式的曲线。这是一个不可修复的漏洞。