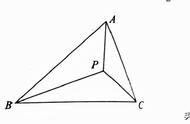
点P在圆外,PQ最长 点P在圆内,PQ最长 点P在圆内,PQ最短
【总结】可见,点与圆的最值问题在本质上仍然是利用了三角形三边关系。

例2.(2019•岐山县一模)如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是_____ .

【解析】如图所示点B′在以E为圆心EA为半径的圆上运动,当D、B′、E共线时时,此时B′D的值最小,
根据折叠的性质,△EBF≌△EB′F,∴EB′⊥B′F,∴EB′=EB,
∵E是AB边的中点,AB=4,∴AE=EB′=2,

例3、如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是弧CD上的一个动点,连接AP,则AP的最小值是_______________.