Prim算法
除了Kruskal算法以外,普里姆算法(Prim算法)也是常用的最小生成树算法。虽然在效率上差不多。但是贪心的方式和Kruskal完全不同。prim算法的核心信仰是:从已知扩散寻找最小。它的实现方式和Dijkstra算法相似但稍微有所区别,Dijkstra是求单源最短路径。而每计算一个点需要对这个点从新更新距离。而prim甚至不用更新距离。直接找已知点的邻边最小加入即可!
对于具体算法具体步骤,大致为:
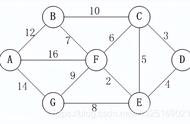
- 寻找图中任意点,以它为起点,它的所有边V加入集合(优先队列)q1,设置一个boolean数组bool[]标记该位置已经确定。
- 从集合q1找到距离最小的那个边v1并判断边另一点p是否被标记(访问),如果p被标记说明已经确定那么跳过,如果未被标(访问)记那么标记该点p,并且与p相连的未知点(未被标记)构成的边加入集合q1,边v1(可以进行计算距离之类,该边构成最小生成树) .
- 重复1,2直到q1为空,构成最小生成树 !
大体步骤图解为:


因为prim从开始到结束一直是一个整体在扩散,所以不需要考虑两棵树合并的问题,在这一点实现上稍微方便了一点。
当然,要注意的是最小生成树并不唯一,甚至同一种算法生成的最小生成树都可能有所不同,但是相同的是无论生成怎样的最小生成树:
- 能够保证所有节点连通(能够满足要求和条件)
- 能够保证所有路径之和最小(结果和目的相同)
- 最小生成树不唯一,可能多样的