代码实现
上面分析了逻辑实现。下面我们用代码简单实现上述的算法。
prim
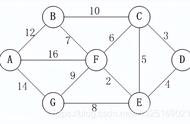
package 图论; import java.util.ArrayList; import java.util.Arrays; import java.util.Comparator; import java.util.List; import java.util.PriorityQueue; import java.util.Queue; public class prim { public static void main(String[] args) { int minlength=0;//最小生成树的最短路径长度 int max=66666; String cityname[]= {"北京","武汉","南京","上海","杭州","广州","深圳"}; int city[][]= { { max, 8, 7, max, max, max, max }, //北京和武汉南京联通 { 8, max,6, max,9, 8,max }, //武汉——北京、南京、杭州、广州 { 7, 6, max, 3,4, max,max }, //南京——北京、武汉、上海、杭州 { max, max,3, max,2, max,max }, //上海——南京、杭州 { max, 9,4, 2,max, max,10 }, //杭州——武汉、南京、上海、深圳 { max, 8,max, max,max, max,2 }, //广州——武汉、深圳 { max, max,max, max,10,2,max }//深圳——杭州、广州 };// 地图 boolean istrue[]=new boolean[7]; //南京 Queue<side>q1=new PriorityQueue<side>(new Comparator<side>() { public int compare(side o1, side o2) { // TODO Auto-generated method stub return o1.lenth-o2.lenth; } }); for(int i=0;i<7;i ) { if(city[2][i]!=max) { istrue[2]=true; q1.add(new side(city[2][i], 2, i)); } } while(!q1.isEmpty()) { side newside=q1.poll();//抛出 if(istrue[newside.point1]&&istrue[newside.point2]) { continue; } else { if(!istrue[newside.point1]) { istrue[newside.point1]=true; minlength =city[newside.point1][newside.point2]; System.out.println(cityname[newside.point1] " " cityname[newside.point2] " 联通"); for(int i=0;i<7;i ) { if(!istrue[i]) { q1.add(new side(city[newside.point1][i],newside.point1,i)); } } } else { istrue[newside.point2]=true; minlength =city[newside.point1][newside.point2]; System.out.println(cityname[newside.point2] " " cityname[newside.point1] " 联通"); for(int i=0;i<7;i ) { if(!istrue[i]) { q1.add(new side(city[newside.point2][i],newside.point2,i)); } } } } } System.out.println(minlength); } static class side//边 { int lenth; int point1; int point2; public side(int lenth,int p1,int p2) { this.lenth=lenth; this.point1=p1; this.point2=p2; } } }
实现效果:

Kruskal:
package 图论; import java.util.Comparator; import java.util.PriorityQueue; import java.util.Queue; import 图论.prim.side; /* * 作者:bigsai(公众号) */ public class kruskal { static int tree[]=new int[10];//bing查集 public static void init() { for(int i=0;i<10;i )//初始 { tree[i]=-1; } } public static int search(int a)//返回头节点的数值 { if(tree[a]>0)//说明是子节点 { return tree[a]=search(tree[a]);//路径压缩 } else return a; } public static void union(int a,int b)//表示 a,b所在的树合并小树合并大树(不重要) { int a1=search(a);//a根 int b1=search(b);//b根 if(a1==b1) {//System.out.println(a "和" b "已经在一棵树上"); } else { if(tree[a1]<tree[b1])//这个是负数,为了简单减少计算,不在调用value函数 { tree[a1] =tree[b1];//个数相加 注意是负数相加 tree[b1]=a1; //b树成为a的子树,直接指向a; } else { tree[b1] =tree[a1];//个数相加 注意是负数相加 tree[a1]=b1; //b树成为a的子树,直接指向a; } } } public static void main(String[] args) { // TODO Auto-generated method stub init(); int minlength=0;//最小生成树的最短路径长度 int max=66666; String cityname[]= {"北京","武汉","南京","上海","杭州","广州","深圳"}; boolean jud[][]=new boolean[7][7];//加入边需要防止重复 比如 ba和ab等价的 int city[][]= { { max, 8, 7, max, max, max, max }, { 8, max,6, max,9, 8,max }, { 7, 6, max, 3,4, max,max }, { max, max,3, max,2, max,max }, { max, 9,4, 2,max, max,10 }, { max, 8,max, max,max, max,2 }, { max, max,max, max,10,2,max } };// 地图 boolean istrue[]=new boolean[7]; //南京 Queue<side>q1=new PriorityQueue<side>(new Comparator<side>() {//优先队列存边 public int compare(side o1, side o2) { // TODO Auto-generated method stub return o1.lenth-o2.lenth; } }); for(int i=0;i<7;i ) { for(int j=0;j<7;j ) { if(!jud[i][j]&&city[i][j]!=max)//是否加入队列 { jud[i][j]=true;jud[j][i]=true; q1.add(new side(city[i][j], i, j)); } } } while(!q1.isEmpty())//执行算法 { side newside=q1.poll(); int p1=newside.point1; int p2=newside.point2; if(search(p1)!=search(p2)) { union(p1, p2); System.out.println(cityname[p1] " " cityname[p2] " 联通"); minlength =newside.lenth; } } System.out.println(minlength); } static class side//边 { int lenth; int point1; int point2; public side(int lenth,int p1,int p2) { this.lenth=lenth; this.point1=p1; this.point2=p2; } } }
kruskal

总结
最小生成树算法理解起来也相对简单,实现起来也不是很难。Kruskal和Prim主要是贪心算法的两种角度。一个从整体开始找最小边,遇到关联不断合并,另一个从局部开始扩散找身边的最小不断扩散直到生成最小生成树。在学习最小生成树之前最好学习一下dijkstra算法和并查集,这样在实现起来能够快一点,清晰一点。
最后,如果你那天真的获得一大笔资金去修建这么一条昂贵的黄金路线,可以适当采取此方法,另外剩下的大批,,苟富贵,勿相忘。。

如果感觉还行,还请点个赞,关注转发分享一下吧