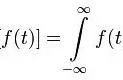就这样,虚数i将数学中最著名的两个数字e和π融合在了一个优雅的等式中。一切豁然开朗,后世物理学家费曼称之为:“我们的珍宝”和“数学中最非凡的公式”。
在科学世界的背景中飘了几百年,虚数最终被主流所接受,并且在19世纪开始大展拳脚,同微积分搭配使用更是能产生意想不到的效果。到了今天,复变函数与积分变换也成了诸多理科生的头疼之源必修法宝。

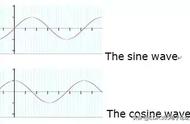
傅里叶变换里还有一个部分,其重要性不低于虚数和微积分,它是谁?就是连小学生都知道的三角函数。
回到傅里叶变换的核心思想:时空中的任何模式都可以被看作不同频率正弦模式的叠加。三角函数在这里充当了拆解后的元件,小巧精致,简洁明了。三角函数当然也是数学世界里的宝物,它历史悠久且从未过时。
不妨先说说为什么会有三角函数:因为直角三角形符合这样一个规律:

这就是毕达哥拉斯定理,它至少有两千年历史。甚至有证据表明,在学者将它总结并书写下来之前,这个规律就已经在匠人之间传播了。它是三角学的基础,也是三角函数的基础。
古人之所以热衷于研究三角学,很大程度上是看中了它对估测巨型实物的帮助,典型应用涉及天文、测绘、航海。从古希腊、古印度,到后来的阿拉伯世界和欧洲,三角学在传播和发展中见证了文明的兴衰。
然而,传统应用往往将三角学局限于具体的几何问题。如果想在更广阔的领域发挥作用,三角函数就需要更灵活的定义。
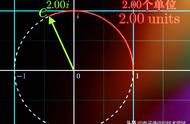
随着解析几何和分析学的出现,人们的视角开始转变。终于,欧拉在18世纪发表了《无穷分析引论》,提出用直角坐标系中的单位圆重塑三角函数的定义。接下来,这些由来已久的概念开始和复数搭档,在级数中出现,于是故事又回到了前面提到过的欧拉公式,当然还有我们言之不尽的傅里叶变换。
关于傅里叶变换,能说的趣事还有很多。比如,傅里叶的热方程和达朗贝尔的波动方程十分神似却又大不相同;比如,傅里叶变换的不同形式;比如,傅里叶与小波,等等。
事实上,每一个方程都是串在历史脉络上的珍珠,它们都是珍宝,也都是寻找其他珍宝的提示。科学的发展环环相扣,很多改变世界的方程都有着密不可分的关系。了解它们的过程像读故事,也像探案,当线索汇集一处,指向未来的时候,你领悟到这本书无法言说的精彩——
推荐阅读

,英国数学科普名家伊恩•斯图尔特经典名作,译为多国语言
李永乐推荐科普读物,“欧拉图书奖”获奖作品
17段改变人类文明进程的数学故事,了解世界运转的深层道理,看懂科学发展的规律