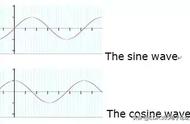
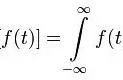图1-2.复音时域波形图
泛音(harmonics)
古希腊人发现了一个有趣的现象,拨弄一下琴弦,这根琴弦除了发出一个响亮的音调外,还会发出一个比这个音调高八度且振幅更小的协和音。在音乐理论中,若一个音的基频为F,则它到它频率两倍(2F)的这个范围就称为“八度”。“高八度”的意思便是基频频率为原来的两倍。换句话讲,他们在八度音程的较低音调中发现了较高音调。而泛音的英文为什么会是“Harmonics”,这是因为琴弦振动产生的声音就是无数简谐波的叠加,最终形成锯齿状的音色。泛音中的基频就是频率最低的那个音的频率,泛音也是一种特殊的复音。

图1-3. 拨动琴弦产生的“锯齿”音色
声与人
振动具有三个很关键的特性:频率、振幅以及相位。一个声音的频率(也就是前文所说的基频)决定了这个声音有多“高”。声波的振幅决定了这个声音有多“响”。相位则代表了声音开始发出的位置。音律是为记录音的“位置”而存在的律学,所以音律研究的重点就是声波的频率。一般来说,人耳能听到的声波频率范围是20赫兹到20000赫兹(每秒振动20000次)。声波的频率越大(每秒振动的次数越多),听起来就越“高”。
但是,我们对音高的线性变化并没有那么敏感,而对音高的指数变化更敏感。举个例子,有如下两个系列的声音:
系列1:
200Hz、400Hz、600Hz、800Hz、1000Hz、1200Hz、1400Hz、1600Hz
系列2:
200Hz、400Hz、800Hz、1600Hz
对于人耳来说,只有系列2的声音听起来像是具有相等距离的,听起来像是一组“等差”音高。可是实际上系列2的声音是一组等比音高。
协和(Consonant)与不协和(Dissonant)
协和(Consonant)用来形容人们听到两个音时的感受,人们将两个音之间的音高差称作音程。所有听起来悦耳、融合的音程,叫协和音程,也说这两个音是协和的;而听起来比较刺耳,彼此不很融合的音程叫做不协和(Dissonant)音程。所以大家可以发现,协和与不协和都是描述人的感受,所以最早得到的哪些音程协和,哪些不协和,都是通过记录无数人的感觉得来的。
那么哪些音程是协和的呢,我们首先来看看两个单音相互作用产生的结果:

图1-4. 在一个临界带宽内两个音的不协和程度
图1-4表示两个单音相互作用的结果。纵坐标为协和、不协和度。横坐标表示两个纯音之间的音程与较低音的临界带宽的比值,这里要介绍一个新概念:临界带宽 (Critical Bandwidth) 。
临界带宽,这个概念首先被Harvey Fletcher在1933年提出,这个概念成功解释了耳蜗听觉滤波效应和掩蔽效应。
人耳具有十分复杂的结构,临界频带指的是由于耳蜗构造产生的听觉滤波器的频率带宽。人的听觉系统中,耳蜗起着频谱分析的作用,耳蜗基底膜上特定位置点对某一特征频率(Characteristic Frequency,CF)的响应最大,当声波偏离CF点时,该点的响应减少,因此基底膜上每一点可等效成具有特定频率(CF)的带通滤波器,整个听觉系统可等效成一系列具有连续CF的、相互交叠的带通滤波器,称为“听觉滤波器”。临界频带就是听觉系统带通滤波功能的反映,听觉滤波器的带宽即为临界带宽。
再回到图1-4,我们可以知道当两个音的音程处于临界带宽内的某一个值时会存在一个最大的不协和的点。由于低频区与高频区临界频带不同,这个位置也不会相同。
但是我们也提到,纯音在自然界上是不存在的。一般都是复音,那么复音之间的协和关系又是怎样呢,早期学者们将图1-4中的线条方程写出来(图1-4的结果是无数实验拟合出来的)再将任意两个复音做傅里叶变换,计算两个音相同次序项之间的协和度,最后加起来就得到了图1-5的结果。并且这个结果也经过了大量的人耳检验。

图1-5. 一个八度内的协和音程关系(采用锯齿音色进行计算得出的结果)
图1-5中描述了一个八度内两个复音的协和音程关系,这两个复音都是前文所提的具有6个谐波叠加的泛音。其中一个的基频为250Hz,它与任意一个频率在250Hz到500Hz内的音的协和关系如图1-5所示。纵坐标表示不协和度,横坐标表示另一个音的基频,这里的单位cps (Cycle per second) 与赫兹意义相同。
从图中我们可以看到在一个八度内协和度最高的就是我们最开始提到的1:1与1:2的比例关系,也就是两个250Hz的音,或者一个250Hz和一个500Hz的音。协和度排第二的是当两个音频率之比为2:3的时候,也就是250Hz与375Hz,这个比例也很重要,与后文要提到的五度相生律有重要关系。
虽然这些严谨数学计算得出的结果在19世纪才出现,但其实在很早的时候,人们就发现了两个音频率之比为2:3的时候,这样的音组十分协和,根据这样的原则,人们开始制定音律。
从五度相生律到十二平均律
早年间,不仅毕达哥拉斯发现了2:3是一个十分协和的频率之比,我国先秦时期的《管子·地员篇》也记载了所谓“三分损益律”,具体说来是取一段弦,“三分损一”,即均分弦为三段,舍一留二,便得到 3/2F(F为弦的原频率)。如果“三分益一”,即弦均分三段后再加一段,便得到 4/3F。“三分损益率”就是最早的音律设计方法。但是如果加上一个4/3F的音,那么他与前面几个音的协和程度就远远不足了。(其实在这里我们可以发现,古人最早发现的协和频率比是2:3和3:4。他们并没有采用比3:4更协和的比例3:5。)所以古人一想,不如找3/2F的3/2倍,也就是9/4 F,但是这个数已经比2还大了,并不在我们要的第一个八度区间[F,2F]中。我们必须找到这个八度里的9/4F,也就是用9/4F除以离他最近的一个整数,也就是2。这样它就变成了9/8F。按照这样的方式,古人在没有计算计算机的情况下一直算到了243/32 F。通过如上的对应关系,形成了最早音律,最终这些比例的频率将一个八度音程分成了七份(如表1-1所示)。