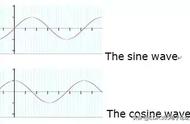
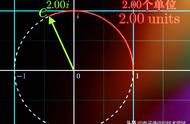
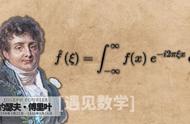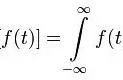其中,式(4)代表一个音和其他音产生的平均场之间的频率差距。式(5)用来计算整个系统的不协和度。为音高为“x”的音的概率,代表所有音与音高“x”的音形成的不协和度的总和,积分区间为(0,1]是因为设定了周期性边界条件,(0,1]代表一个八度,积分函数都满足这个周期性的边界条件。最后式(6)表示的是这个系统的熵。
其中,因为概率是一个周期函数,所以很容易想到使用傅里叶级数作为他的表达式。可以将其写成:


图2-2. (A)当时,计算的锯齿音色不同频率差的两个音的非协和度(图中展示了两个八度)。(B)通过(A)图的非协和度计算出来的公式(8)的每一项的参数d。
那么,既然所有参数都设置好了,我们就要开始最小化自由能了。在这个系统中,温度T只是一个参数,并不代表真实温度。我们如果去模拟一个T不断变小的降温过程,并且在每一个T下都使得系统的亥姆霍兹自由能最小时,这个系统中的音的频率分布会是怎样的呢?

图2-3. 随着“温度”下降,一个八度内声音概率密度的变化
如图2-3纵坐标表示音的概率密度,纵坐标越大说明在一个八度内具有某个基频音的数量越多,令人惊喜的是,在T=20.2、T=16.3时,都能看到12个概率相同的尖峰。这说明:若是某一个音乐系统,要具有最小的非协和度,同时要足够复杂时,只需要在一个八度内形成一个有十二项的“等差”音高就行!这正好对应着“十二平均律”的出现。而在T小于16.2时,可以看到12个不同概率的峰出现,这也对应着早期具有12声音阶的纯律。