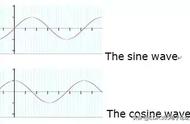
如果有学过傅立叶级数,对这个等式就会有似曾相识的感觉,不错!这个等式跟傅立叶级数是非常相似的:

当然,差别是肯定是存在的,因为这两个等式是在两个不同条件下运用的,至于怎么证明DFT合成公式,这个我想需要非常强的高等数学理论知识了,这是研究数学的人的工作,对于普通应用者就不需要如此的追根究底了,但是傅立叶级数是好理解的,我们起码可以从傅立叶级数公式中看出DFT合成公式的合理性。
_ _
DFT合成等式中的Im X[k]和Re X[k]跟之前提到的Im X[k]和Re X[k]是不一样的,下面是转换方法(关于此公式的解释,见下文):

但k等于0和N/2时,实数部分的计算要用下面的等式:

上面四个式中的N是时域中点的总数,k是从0到N/2的序号。
为什么要这样进行转换呢?这个可以从频谱密度(spectral density)得到理解,如下图就是个频谱图: