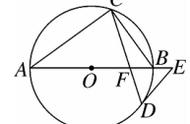
发现已知条件BD与BE都在三角形BDO中,而三角形BDO是一个直角三角形,OD的长度可以设成是半径r,而OE的长度也是半径。在三角形BDO中用一下勾股定理,也就是根号3的平方加r的平方等于斜边1+r的平方,那样半径就可以得到。
将这个式子展开,3+r的平方等于1+2r+r万,两边都有方,抵消掉以后2r=3-1,所以半径等于1。半径等于1以后将r替换掉,以后发现三角形BDO正好是30度的直角三角形。因为OD等于1,BO等于2,正好是一,二,根号3这个三角形。

由于角B等于角C都是30度,所以角DOB等于60度。而三角形CMO与三角形BDO是全等的,所以角MOC也是60度,那样就可以得到圆心角,圆心角的度数就是180度,减坐边的60度,再减掉右边的60度,也是60度。

而三角形ADO与三角形AMO是全等的,所以对于三角形AOM采说也是一个顶角,有一个角是30度的直角三角形,OM就是半径1,所以30度,角AOM是30度,那么taf30度就等于AM比1,所以AM的长度就可以得到,是3分之根号3。
AM的长度有了以后直接往这个式子里带就可以了,是2乘以1/2,再乘以3分之根号3,再乘以1,然后减掉扇形的面积,扇形面积是60/360,π2方。也就是π1的平方。将这个式子处理一下以后,2与2约分,这里是3分之根号3,减掉360分60,1/6然后π1的平方,6分之π,这个题就得到了解决。

这个题第一问比较麻烦,第一问必须要知道做垂直证半径,或者是做半径证垂直,切线的证明是这两种方法。还有一个要熟练的运用30度的直角三角形三边之间的关系,或者是三角函数数值。
本期视频就到这里,希望对同学们有所帮助。